

|
| Elliott Sound Products | Beginners' Guide to Electronics - Part 1 |
 Main Index Main Index
 Articles Index Articles Index
|
Having looked at some of the alternative offerings on the web, I decided it was time to do a series on basic electronics. Most I have seen are either too simplistic, and do not explain each component well enough, or are so detailed that it is almost impossible to know what you need to know as opposed to what you are told you need. These are usually very different.
Basic components are not always as simple as they may appear at first look. This article is intended for the beginner to electronics, who will need to know a number of things before starting on even the simplest of projects. The more experienced hobbyist will probably learn some new things as well, since there is a good deal of information here that most non-professionals will be unaware of.
This is by no means an exhaustive list, and I shall attempt to keep a reasonable balance between full explanations and simplicity. I shall also introduce some new terminology as I go along, and it is important to read this the way it was written, or you will miss the explanation of each term as it is first encountered.
One thing you will need is a decent scientific calculator. Those on mobile (cell) phones are usually inadequate, but scientific calculators are available at very low cost. You won't use (or need) most of the functions, but some are essential - logarithmic operations, square root and raising numbers to powers (e.g. 10^8) are used regularly.
It must be noted that some US authors (as well as a few from elsewhere) still retain some very antiquated terminology, and this often causes great confusion for the beginner (and sometimes the not-so-beginner as well). You will see some 'beat-ups' of the US - citizens of same, please don't be offended, but rather complain bitterly to anyone you see using the old terminology.
Within The Audio Pages, I use predominantly European symbols and terminology - these are also the recommended (but not mandatory) symbols and terms for Australia, and I have been using them for so long that I won't be changing anything.
The basic electrical units and definitions are as shown below. This list is not exhaustive (also see the Glossary), but covers the terms you will encounter most of the time. Many of the terms are somewhat inter-related, so you need to read all of them to make sure that you understand the relationship between them.
Passive: Capable of operating without an external power source. Typical passive components are resistors, capacitors, inductors and diodes (although the latter are a special case).
Active: Requiring a source of power to operate. Includes transistors (all types), integrated circuits (all types), TRIACs, SCRs, LEDs, etc.
DC: Direct Current The electrons flow in one direction only. Current flow is from negative to positive, although it is often more convenient to think of it as from positive to negative. This is sometimes referred to as 'conventional' current as opposed to electron flow.
AC: Alternating Current The electrons flow in both directions in a cyclic manner - first one way, then the other. The rate of change of direction determines the frequency, measured in Hertz (cycles per second).
Frequency: Unit is Hertz, Symbol is Hz, old symbol was cps (cycles per second), f is used in formulae to denote frequency in Hz A complete cycle is completed when the AC signal has gone from zero volts to one extreme, back through zero volts to the opposite extreme, and returned to zero. The accepted audio range is from 20Hz to 20,000Hz. The number of times the signal completes a complete cycle in one second is the frequency.
Voltage: Unit is Volts, Symbol is V or U, old symbol was E (from EMF - electromotive force) Voltage is the 'pressure' of electricity, or 'electromotive force' (hence the old term E). A 9V battery has a voltage of 9V DC, and may be positive or negative depending on the terminal that is used as the reference. The mains has a nominal voltage of 230 or 120V depending where you live - this is AC, and alternates between positive and negative values. Voltage is also commonly measured in millivolts (mV), and 1,000 mV is 1V. Microvolts (µV), nanovolts (nV), kilovolts (kV) and megavolts (MV) are also used.
Current: Unit is Amperes (Amps), Symbol is I Current is the flow of electricity (electrons). No current flows between the terminals of a battery or other voltage supply unless a load is connected. The magnitude of the current is determined by the available voltage, and the resistance (or impedance) of the load and the power source. Current can be AC or DC, positive or negative, depending upon the reference. For electronics, current may also be measured in mA (milliamps) - 1,000 mA is 1A. Nanoamps (nA) are also used in some cases.
Resistance: Unit is Ohms, Symbol is R or Ω Resistance is a measure of how easily (or with what difficulty) electrons will flow through the device. Copper wire has a very low resistance, so a small voltage will allow a large current to flow. Conversely, the plastic insulation has a very high resistance, and prevents current from flowing from one wire to those adjacent. Resistors have a defined resistance, so the current can be calculated for any voltage. Resistance in passive devices is always positive (i.e. > 0)
Conductance: Unit is Siemens, Symbol is S Conductance (symbol 'G') is generally associated with valves (vacuum tubes) and FETs (field effect transistors). The original unit was the 'mho' (ohm spelled backwards). Conductance, susceptance, and admittance are the reciprocals of resistance, reactance, and impedance respectively. One Siemens is equal to the reciprocal of one ohm. Conductance etc. are not covered here.
Capacitance: Unit is Farads, Symbol is C or F (depending on context) Capacitance is a measure of stored charge. Unlike a battery, a capacitor stores a charge electrostatically rather than chemically, and reacts much faster. A capacitor passes AC, but will not pass DC (at least for all practical purposes). The reactance or AC resistance (called impedance) of a capacitor depends on its value and the frequency of the AC signal. Capacitance is always a positive value.
Inductance: Unit is Henrys, Symbol is H or L (depending on context) Inductance occurs in any piece of conducting material, but is wound into a coil to be useful. An inductor stores a charge magnetically, and presents a low impedance to DC (theoretically zero), and a higher impedance to AC dependent on the value of inductance and the frequency. In this respect it is the electrical opposite of a capacitor. Inductance is always a positive value. The symbol 'Hy' is sometimes used in the US. There is no such symbol in the definitions.
Impedance: Unit is Ohms, Symbol is Ω or Z Unlike resistance, impedance is a frequency dependent value, and is specified for AC signals. Impedance is made up of a combination of resistance, capacitance, and/ or inductance. In many cases, impedance and resistance are the same (a resistor for example). Impedance is most commonly positive (like resistance), but can be negative with some components or circuit arrangements.
Decibels: Unit is the Bel, but because this is large, deci-Bels (1/10 th Bel) are used), Symbol is dB Decibels are used in audio because they are a logarithmic measure of voltage, current or power, and correspond well to the response of the ear. A 3dB change is half or double the power (0.707 or 1.414 times voltage or current respectively). Decibels are discussed more thoroughly in a separate section (see Frequency, Amplitude & dB).
A few basic rules that electrical circuits always follow are useful before we start.
Some of these are intended to forewarn you against some of the outrageous claims you will find as you research these topics further, and others are simple electrical rules that apply whether we like it or not.
There are many different representations for basic wiring symbols, and these are the most common. Other symbols will be introduced as we progress.
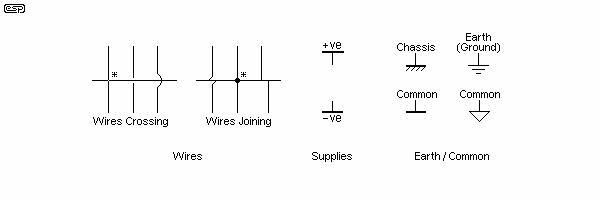
The conventions I use for wires crossing and joining are marked with a star (*) - the others are a small sample of those in common use, but are fairly representative. Many can be worked out from their position in the circuit diagram (schematic). Some schematics will be found where it is unclear whether conductors shown are joined or not. It will sometimes be easy enough to determine which is which with enough knowledge and experience, but some drawings are so bad that it can be almost impossible.
The commonly accepted units in electronics are metric. In accordance with the SI (System Internationale) metric specifications, any basic unit (such as an Ohm or Farad) will be graded or sub-graded in units of 1,000 - this gives the following table.
| Term | Abbreviation | Value (Scientific) | Value (Normal) |
| Tera | T | 1 x 1012 | 1,000,000,000,000 |
| Giga | G | 1 x 109 | 1,000,000,000 |
| Mega | M | 1 x 106 | 1,000,000 |
| kilo | k (lower case) | 1 x 103 | 1,000 |
| Units | - | 1 | 1 |
| Milli | m | 1 x 10-3 | 1 / 1,000 |
| Micro | μ or u | 1 x 10-6 | 1 / 1,000,000 |
| Nano | n | 1 x 10-9 | 1 / 1,000,000,000 |
| Pico | p | 1 x 10-12 | 1 / 1,000,000,000,000 |
The abbreviations and case are important - 'm' is quite clearly different from 'M'. In general, values smaller than unity use lower case, and those greater than unity use upper case. 'k' is clearly an exception to this. There are others that go above and below those shown, but it is unlikely you will encounter them. Even Giga and Tera are somewhat unusual in electronics (except for determining the size hard drive needed to install a Microsoft application  ).
).
In most electronics work, the number of formulae is not as great as you might have imagined. While basic addition, subtraction, multiplication and division cover most of the things you'll need, there are a couple of exceptions. Whether you really need them depends on what you're doing.
Ohm's LawOf all the formulae, Ohm's law is by far the most all-pervasive. It's rare that you'll find anything in electronics where it's not needed. There is a simple 'transposition triangle' shown below that is designed to help you to rearrange the formula to determine the unknown value. Ohm's law states ...
R = V / I Where R is resistance, V is voltage and I is current (this is covered in detail in section 5.0 below)
Kirchhoff's laws are less well known than those of Mr Ohm. Provided that you understand the concepts, you understand the laws whether you remember who's laws they are or not. They are not formulae, but a pair of statements of fact that (hopefully) make perfect sense.
Current Law - The algebraic sum of all currents entering and exiting a node must equal zero.
Voltage Law - The algebraic sum of all voltages in a closed loop must equal zero.
If this doesn't do anything for you, don't worry too much about it because it usually takes care of itself when you analyse a circuit.
Reactance is less common but no less important. Reactive components are capacitors and inductors, with capacitors being much closer to being a 'pure' reactance than inductors. The latter have internal resistance due to the coil of wire and stray (distributed) capacitance between adjacent turns. This causes their behaviour to deviate from 'ideal' (i.e. a component that has only the desired characteristics). Most resistors are close to ideal at audio frequencies, as are most capacitors (excluding electrolytic types). Reactance is determined by two different formulae - one for capacitors and another for inductors ...
| Xc = 1 / ( 2π × f × C ) | Where Xc is capacitive reactance, π is 3.141592654, f is frequency (in Hz) and C is capacitance (in Farads). | |
| Xl = 2π × f × L | Where Xl is inductive reactance and L is inductance (in Henrys). Other terms as above. |
You will often see the symbol ω in formulae, particularly those where capacitance and/ or inductance are used. ω (lower case omega) simply means the 'angular frequency' in radians per second, which is 2π × f (often written simply as 2πf). The lower case omega should not be confused with the Upper Case symbol ( Ω ) which is the symbol for ohms. Note that these symbols are used elsewhere in mathematics where they may have very different meanings. We are interested only in the meanings as they apply to electronics.
When capacitors and inductors are combined, a resonant circuit is created. Resonance is calculated by the following formula ...
| of = 1 / ( 2π × √ (L × C )) | Where of is resonant frequency, L is inductance (Henrys) and C is capacitance (Farads). |
Squares and square roots ( √ ) feature heavily in electronics. You need a calculator that can provide square roots, as they are so common. One of the most useful is the square root of 2 ( √2 = 1.414 ) and its reciprocal ( 1 / √2 = 0.707 ). These are applied to the most basic of all waveforms - the sinewave.
| VRMS = Vpeak × 0.707 | or ... | |
| Vpeak = VRMS × 1.414 |
Power calculations are necessary to work out the dissipation of any device that has voltage across it and current flowing through it. Capacitors and inductors are the (partial) exceptions, because they are reactive. Only the purely resistive part of reactive components is relevant, the winding resistance of an inductor or the ESR (equivalent series resistance) of a capacitor. Inductors with steel or ferrite cores are also subject to saturation, but calculating that is well outside the scope of this article.
Power can be calculated several ways, but with AC there are some anomalies (caused by reactance) that mean that 'true' power can be difficult to calculate. Again, that's outside the scope of this article, but the ESP website does have extensive information if you need it. See Power Factor to learn more. For DC calculations and purely resistive AC calculations, power is calculated by ...
| P = V × I | Where P is power in watts, V is voltage, I is current. | |
| P = V ² / R | R is resistance. | |
| P = I ² × R |
For those electronics enthusiasts who are also into music (a very common combination), the 12 th root of 2 is often useful. This computes the interval needed to divide an octave into 12 semitones. The number is 1.059463094 but it's hardly something that will be memorised. To calculate it, use the formula ...
| 2^ ( 1 / 12 ) | 2 raised to the power of ( 1 / 12 ) | Which gives 1.059463094 |
If you multiply A440 (concert pitch 'A', 440Hz) by 1.059463094 exactly 12 times, you get 880Hz - one octave higher than 440Hz. The frequencies are as follows ...
440 Hz, 466.1637615, 493.8833013, 523.2511306, 554.365262, 587.3295358, 622.2539674, 659.2551138, 698.4564629, 739.9888454, 783.990872, 830.6093952, 880 Hz
The same process can be used to divide an octave into any number of divisions. A 1/3 octave graphic equaliser (for example) simply means that the starting frequency is multiplied by 2^ ( 1 / 3 ) (1.25992105). Predictably, a 1/2 octave equaliser uses a figure of 2^ ( 1 / 2 ) which is the same as √2 - 1.414 (it pops up in the most unexpected places  ).
).
Another set of formulae that you may need (depending on the kind of things that interest you) are to do with wavelength. This is important for determining antenna sizes (for RF work), or for working out some of the more obscure acoustic properties of loudspeaker drivers. For example, the diameter of a cone speaker should generally be less than one wavelength at the highest frequency it reproduces. Wavelength is represented by the symbol 'λ' (lambda). You need to know velocity and frequency to determine the wavelength of a waveform. Velocity depends on the medium and nature of the wave.
Sound waves in air travel at 343m/s (dry air at sea level and ~20°C), and radio waves or light travel at 3E8m/s (also written as 3 × 10^8m/s ). Light and electrical signals in air or a vacuum travel at the same speed regardless of temperature, but electrical signals travel slower in coaxial cables or waveguides. This is called the 'velocity factor'. More info on that can be found in the article Coaxial Cables and isn't covered here.
| C = (331.3 + 0.606) × °C | Velocity in dry air (0% humidity), where °C is ambient temperature. | |
| Wavelength (λ) = C / f | Where C is velocity and f is frequency. |
A 1kHz sinewave as sound (in air) has a wavelength of 343mm, and a 10MHz radio wave in air or a vacuum has a wavelength of 30 metres. If travelling in a coaxial cable, the radio wave may have its wavelength extended to 40 metres (a velocity factor of 0.75). These facts are useful to know, but don't need to be memorised (as long as you know where to find them again).
Finally, we'll examine decibels (dB). This topic has its own page (Frequency, Amplitude & dB), but the formulae are shown here for the sake of (relative) completeness. We use dB so often in electronics that it's very hard to avoid the subject. It's also confusing for beginners (and some experienced people as well) to get your head around logarithmic functions - although all our senses are log, we don't think of them that way. Decibels were introduced to make the enormous range of acoustic levels we can hear into something more rational.
| dB = 20 × log ( V1 / V2 ) | Where V1 and V2 are two voltage (or current) values. | |
| dB = 10 × log ( P1 / P2 ) | Where P1 and P2 are two power values. |
Whether the dB level is positive or negative depends on whether the circuit has gain or loss respectively. We can hear (for a young person with undamaged hearing) a range of well over 120dB, which is a pressure variation (the acoustical equivalent of voltage) of 1,000,000 to one. Using dB makes it a lot easier to cope with such large numbers, and knowing that a 10dB difference (voltage or power) is heard as twice or half as loud makes it all fall into place.
The formulae shown above are by no means all that you'll ever see, but they are enough to get you well under way to understanding what's going on. There is more info further on (especially in the 'Circuits In Combination' section below).
There are many other formulae that you'll likely need, such as imperial to metric conversion. Temperature is one, and while a couple of countries still use Fahrenheit, almost everyone uses Celsius. I'll only show the conversion to Celsius, as there's no reason to use its inverse. Kelvin is often found, with 0K being the absence of all heat (and molecular movement). Note that there are no 'degrees' with Kelvin, so 273K is just under 20°C. Apart from the zero point, a temperature change of 1K is 1°C.
0K = -253.15°C
°'C = (°F - 32) x 5 / 9
Temperatures are always shown in Celsius on the ESP website, but you will also see (for example) 5K/W specified for thermal resistance. This is the same as 5°C/W, and you'll often see K/W used in semiconductor datasheets.
I generally show all size measurements in millimetres (mm), but sometimes these are 'odd' numbers because they are translated from inches for PCB layouts. I've only shown three basic conversions, and you can work out any others that you need.
1" = 25.4mm
1' = 304.8mm
0.1" = 2.54mm
Large distances are not included, but you can use an online calculator to convert just about any distance to another format. This can also be used with velocity, so if you see velocity specified in furlongs/ fortnight ¹, that's roughly 1.663×10-4 m/s, (i.e. 0.1663 mm/s). No, you won't find this type of measurement on the ESP site. 
¹ Humorous Units of Measurement (Wikipedia)
Resistors in series are easy - just add up the values to get the total. This works with inductors as well. Capacitors in parallel also just add together. When you have resistors or inductors in parallel (or caps in series), there are several ways to determine the value. The most common (and it works with multiple values) is based on reciprocals. It's actually the 'reciprocal of the sum of reciprocals' and while that's a mouthful, it's the most flexible method.
I've only shown resistances here, but you can substitute inductance (in parallel) or capacitance (in series). The formulae all work, so decide on your favourite and stick with it.
For example ...
R = (1 / (1 / R1) + (1 / R2) + (1 / R3) (1 / etc.)) For example, with 1k and 10 ohms in parallel ...
R = (1 / (1 / 1k) + (1 / 10)) = 9.901Ω
Another common method (that only works with two values) is ...
R = (R1 × R2) / (R1 + R2) Using the same values ...
R = ( 10k ) / 1.01k = 9.901Ω
Yet another technique is the 'N+1' rule. This is less common than the others, and again only works with two values ...
R1 = 1k, R2 = 10Ω
N+1 = 1k / 10 + 1 = 101
R = R1 / (N + 1) = 1k / 101 = 9.901Ω
When resistors are in parallel, the end result must be lower than the lowest (or lower) value. The same applies to capacitors in series. These techniques are all useful, and I leave it to the reader to decide which formula s/he prefers. Personally, I almost always use the 'reciprocals' method, because it works with multiple values. It is irksome to do with a calculator though, and if you only have two values, the 'N+1' method is by far the easiest.
The first and most common electronic component is the resistor. There is virtually no working circuit I know of that doesn't use them, and a small number of practical circuits can be built using nothing else. There are three main parameters for resistors, but only two of them are normally needed, especially for solid state electronics.
The resistance value is specified in ohms, the standard symbol is 'R' or Ω. Resistor values are often stated as 'k' (kilo, or times 1,000) or 'M', (meg, or times 1,000,000) for convenience. There are a few conventions that are followed, and these can cause problems for the beginner. To explain - a resistor has a value of 2,200 Ohms. This may be shown as any of these ...
The use of the symbol for Ohms (Omega, Ω is optional, and is most commonly left off, since it is irksome to add from most keyboards. The letter 'R' and the '2k2' conventions are European, and were not commonly seen in the US, UK, Australia, etc. until recently. Other variants are 0R1, for example, which means 0.1 Ohm. You may also see 0E1 which means the same. SMD (surface mount device) resistors generally use a 3-digit code, such as 222 shown above. The first two digits indicate the basic value (22) and the third shows the number of zeros. 2k2 is therefore 222, and 22k is 223 (three zeros). These are sometimes used on schematics, which isn't helpful.
The schematic symbols for resistors are either of those shown below. I use the Euro version of the symbol exclusively.
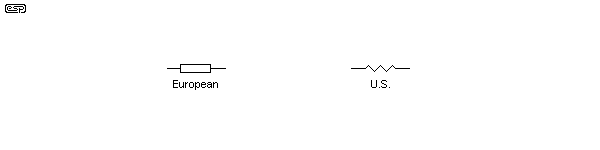
The basic formula for resistance is Ohm's law, which states that ...
1.1.1 R = V / I Where V is voltage, I is current, and R is resistance
The other formula you need with resistance is Power (P)
1.1.2 P = V² / R
1.1.3 P = I² × R
The easiest way to transpose any formula is what I call the 'Transposition Triangle' - which can (and will) be applied to other formulae. The resistance and power forms are shown below - just cover the value you want, and the correct formula is shown. In case anyone ever wondered why they had to do algebra at school, now you know - it is primarily for the manipulation of a formula - they just don't teach the simple ways. A blank between two values means they are multiplied, and the horizontal line means divide.
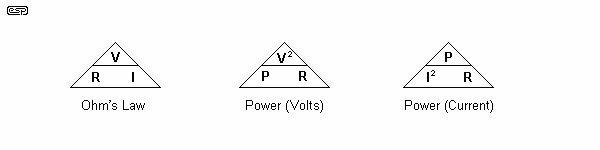
Needless to say, if the value you want is squared, then you need to take the square root to get the actual value. For example, you have a 100 Ohm, 5W resistor, and want to know the maximum voltage that can be applied. V² = P × R = 500, and the square root of 500 is 22.36, or 22V. This is the maximum voltage across the resistor to remain within its power rating. In some cases you need to de-rate the resistor to account for ambient temperature, so a 5W resistor may only be able to dissipate 2.5W if the surrounding temperature is too high.
 | Please note that 'ambient temperature' always means the temperature around a component, such as inside the enclosure or the temperature next to a part that runs hot. It does not mean the temperature in the room, outside, or at a random location in Outer Mongolia. This is a common mistake (with the possible exception of Outer Mongolia), and can cause unexpected failures due to over-temperature. Valve amplifiers are a case in point, because everything near the valves gets hot, and this is the ambient temperature! |
Resistors have the same value for AC and DC - they are not frequency dependent within the normal audio range. Even at radio frequencies, they will tend to provide the same value, but at very high frequencies other effects become influential. These characteristics will not be covered, as they are outside the scope of this article.
A useful thing to remember for a quick calculation is that 1V across a 1k resistor will have 1mA of current flow - therefore 10V across 1k will be 10mA (etc.).
There are a number of different standards, commonly known as E12, E24, E48, E96 and E192, meaning that there are 12, 24, 48 96 or 192 individual values per decade (e.g. from 1k to 10k). The most common, and quite adequate for 99.9% of all projects, are the E12 and E24 series. I've included the E48 series in the following tables, but I don't intend to add the E96 or E192 values. These are not as readily available as the others, but be aware that many suppliers will not have the full E48 range as a stock item, and the E96 values are less common again.
The E12 series (roughly) follows a progression based on the 12th root of 10 (1.2115), to obtain 12 values per decade. Other series use the same technique. This is based on the familiar (to musicians at least) 12th root of 2 (1.05946) which divides an octave into 12 semitones. No, you don't need to remember any of this, it's included only to show how the values came about (and it's interesting)  . E3 and E6 ranges used to be available, but are long gone (the values can still be obtained from higher series, but with tighter tolerance).
. E3 and E6 ranges used to be available, but are long gone (the values can still be obtained from higher series, but with tighter tolerance).
According to IEC 60063, The E12, E24 and E48 series follow these sequences (each covers one decade, and values span about five decades from 10Ω to 1MΩ) ...
| 10 | 12 | 15 | 18 | 22 | 27 | 33 | 39 | 47 | 56 | 68 | 82 |
| 10 | 12 | 15 | 18 | 22 | 27 | 33 | 39 | 47 | 56 | 68 | 82 | ||||||||||||
| 11 | 13 | 16 | 20 | 24 | 3.0 | 36 | 43 | 51 | 62 | 75 | 91 |
| 100 | 121 | 147 | 178 | 215 | 261 | 316 | 3.83 | 464 | 562 | 681 | 825 |
| 105 | 127 | 154 | 187 | 226 | 274 | 332 | 4.02 | 487 | 590 | 715 | 866 |
| 110 | 133 | 162 | 196 | 237 | 287 | 348 | 4.22 | 511 | 619 | 750 | 909 |
| 115 | 140 | 169 | 205 | 249 | 301 | 365 | 4.42 | 536 | 649 | 787 | 953 |
Long ago, resistors were available with a 20% tolerance, but most are now 5% or better. Generally, 5% resistors will follow the E12 sequence, and 1% or 2% resistors will be available in the E24 sequence. Wherever possible in my projects, I use E12, as these are commonly available almost everywhere. 1% resistors are readily available from most suppliers in the E12 and E24 series. There are also E48 (48 values per decade, Table 5.3), E96 and even E192 ranges, and some designers use the extended ranges to ensure close tolerance (the nominal tolerance for E96 resistors is 1%, but E24 values are readily available with 1% tolerance).
Note that some of the E12 and E24 values are not available in the E48 series, and the same applies to the E96 and E192 series. This isn't a limitation, since these values are already provided in 'lesser' series. For example, if you're using the E48 range, you won't get a 3.3k resistor, so if that's what you need you'll get it from the E12 or E24 series instead. Also be aware that E48 series values are generally comparatively expensive, especially if you get 0.1% tolerance types.
Resistors are available in multiple decades, with values ranging from 0.1 Ohm (0R1) up to 10M Ohms (10,000,000 Ohms) or more. There are also resistors much lower than 0.1Ω and up to several GΩ (1 gigaohm = 1,000 MΩ). Not all values are available in all types, and close tolerances are uncommon in very high and very low values. Most values are available from 10Ω up to 1MΩ, but the number of values below and above these limits is generally restricted. Don't expect to be able to buy a 1.05Ω or 6.19MΩ resistor (for example).
SMD (surface mount) resistors are often marked using a 3 digit code. The first two digits are the value (e.g. 22x or 47x) and the third number is the number of zeros that follow. The value is in ohms, so 222 means 2200 ohms = 2.2k or 2k2. The same code is used on many capacitors (see below).
5.2 Colour Codes
Low power (≤ 2W) resistors are nearly always marked using the standard colour code. This comes in two variants - 4 band and 5 band. The 4 band code is most common with 5% and 10% tolerance, and the 5 band code is used with 1% and better.
| Colour | 1 st Digit | 2 nd Digit | 3 rd Digit | Multiplier | Tolerance |
| Black | 0 | 0 | 0 | 1 | |
| Brown | 1 | 1 | 1 | 10 | 1% |
| Red | 2 | 2 | 2 | 100 | 2% |
| Orange | 3 | 3 | 3 | 1,000 | |
| Yellow | 4 | 4 | 4 | 10,000 | |
| Green | 5 | 5 | 5 | 100,000 | |
| Blue | 6 | 6 | 6 | 1,000,000 | |
| Violet | 7 | 7 | 7 | ||
| Grey | 8 | 8 | 8 | ||
| White | 9 | 9 | 9 | ||
| Gold | 0.1 | 5% | |||
| Silver | 0.01 | 10% |
My apologies if the colours look wrong - blame the originators of the 'standard' HTML colours ... or your monitor. With the 4 band code, the third digit column is not used, it is only used with the 5 band code. This is somewhat confusing, but we are unable to change it, so get used to it. Personally, I suggest the use of a multimeter when sorting resistors - I know it's cheating, but at least you don't get caught out by incorrectly marked components (and yes, this does happen).
5.3 Tolerance
The tolerance of resistors is mostly 1%, 2%, 5% and (now rarely for most types) 10%. In the old days, 20% was also common, but these are now rare. Even 10% resistors are hard to get except in some types and for extremely high or low values (> 10M or < 1R), where they may be the only options available at a sensible price. You can always use resistors with closer tolerance than specified in a circuit, and you can select values that are closest to the one you want from 5% or 10% resistors.
A 100R resistor with 5% tolerance may be anywhere between 95 and 105 ohms - in most circuits this is insignificant, but there will be occasions where very close tolerance is needed (e.g. 0.1% or better). This is fairly uncommon for audio, but there are a few instances where you may see such close tolerance components. They are not always needed, but you have to understand the circuit to know whether the difference is significant or not.
5.4 Power Ratings
Resistors are available with power ratings of 1/8th W (or less for surface mount devices), up to hundreds of watts. The most common are 1/4W (0.25W), 1/2W (0.5W), 1W, 5W and 10W. Very few projects require higher powers, and it is often much cheaper to use multiple 10W resistors than a single (say) 50W unit. They will also be very much easier to obtain.
Like all components, it is preferable to keep temperatures as low as possible, so no resistor should be operated at its full power rating for any extended time. I recommend a maximum of 0.5 of the power rating wherever possible. Wirewound resistors can tolerate severe overloads for a short period, but I prefer to keep the absolute maximum to somewhat less than 250% - even for very brief periods, since they may become open circuit from the stress (and/ or thermal shock) rather than temperature (this does happen, and I have experienced it during tests and repairs). In some cases, higher than expected power ratings might be specified to ensure that the resistor(s) will survive continuous high voltages.
5.5 Resistance Materials
Resistors are made from a number of different materials. I shall only concentrate on the most common varieties, and the attributes I have described for each are typical - there will be variations from different makers, and specialised types that don't follow these (very) basic characteristics. All resistors are comparatively cheap.
A couple of points to ponder. Resistors make noise! Everything that is above 0K (zero Kelvin, absolute zero, or -273°C - degrees Celsius) makes noise, and resistors are no exception. Noise is proportional to temperature and voltage. Low noise circuits will always use low resistor values and low voltage wherever possible. The noise created by an ideal resistor (zero excess noise) is determined from the following formula ...
VR = √ ( 4k × T × B × R )
Where ...
VR = resistor's noise voltage
k = Boltzmann constant (1.38E-23)
T = Absolute temperature (Kelvin)
B = Noise bandwidth in Hertz
R = Resistance in ohms
The noise generated by any conductor can be calculated. A 1kΩ resistor has a noise output of roughly 4nV/√Hz (.565µV for 20kHz bandwidth). More information is available in the article Noise In Audio Amplifiers.
Resistors may also have inductance, and wirewound types are the worst for this. There are non-inductive wirewound resistors, but are not readily available, and usually not cheap. There are also resistors marked and sold as non-inductive, but are re-badged standard resistors. I expect you can guess where they come from.
All resistors have a maximum voltage limit, and it's not simply based on the dissipated power. For example, a 1MΩ, 0.25W (250mW, 1/4W) resistor is theoretically able to handle 500V while not exceeding its maximum dissipation. A 10MΩ resistor of the same size can therefore handle over 1.5kV ... except it cannot! The spacing between the spiral cut made in the resistance material may simply arc, and the insulation layer will not be designed for such a high voltage.
It's usually hard to find the voltage rating for resistors - it's in the datasheet, but that assumes that you have access to the datasheet for the resistors you are using. In most cases (and subject to dissipation), aim for no more than 200V across any 'standard' through-hole resistor if you don't have any other data available. Many common 250mW metal film resistors may have a rated voltage of up to 350V, but others may be lower and a few higher. It's very common in high-voltage (e.g. 400V DC) circuits to see two or three (equal value) resistors used in series. That ensures that the voltage across each is kept low enough to ensure there is no premature degradation of the resistors.
Anyone who has worked on valve equipment will have seen resistors that have gone high - their resistance has increased, often to more than double the rated value. This is usually due to excessive voltage, but it can also happen simply due to age with carbon film resistors. In many cases, you'll see 1W resistors used where the dissipation is only a fraction of that. This is done because 1W resistors are physically larger, so can withstand a higher voltage before they fail.
As shown in the previous section, running resistors hot increases their noise output as well as reducing their expected life. With all electronic parts, the cooler they run, the longer they last.
Capacitors come in a bewildering variety of different types. The specific type may be critical in some applications, where in others, you can use anything you please. Capacitors are the second most common passive component, and there are few circuits that do not use at least one capacitor.
A capacitor is essentially two conductive plates, separated by an insulator (the dielectric). To conserve space, the assembly is commonly rolled up, or consists of many small plates in parallel for each terminal, each separated from the other by a thin plastic film. See below for more detailed information on the different constructional methods. A capacitor also exists whenever there is more than zero components in a circuit - any two pieces of wire will have some degree of capacitance between them, as will tracks on a PCB, and adjacent components. Capacitance also exists in semiconductors (diodes, transistors), and is an inescapable part of electronics.
There are two main symbols for capacitors, and one other that is common in the US, but rarely seen elsewhere. Caps (as they are commonly called) come in two primary versions - polarised and non-polarised. Polarised capacitors must have DC present at all times, of the correct polarity and exceeding any AC that may be present on the DC polarising voltage. Reverse connection will result in the device failing, often in a spectacular fashion, and sometimes with the added excitement of flames, or high speed pieces of casing and electrolyte (an internal fluid in many polarised caps). This is not a good thing.
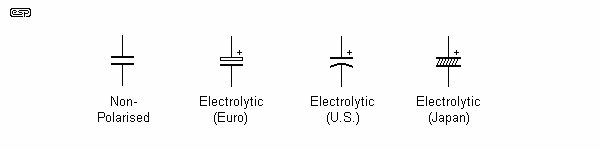
Capacitors are rated in Farads, and the standard symbol is 'C' or 'F', depending upon the context. A Farad is so big that capacitors are most commonly rated in micro-Farads (µF). The Greek letter (lower case) Mu (µ) is the proper symbol, but 'u' is available on keyboards, and is far more common. Because of the nature of capacitors, they are also rated in very much smaller units than the micro-Farad - the units used are ...
The items in bold are the ones I use in all articles and projects, and the others (especially mfd, MFD, ufd, UFD, mmf and/or MMF) should be considered obsolete and not used - at all, by anyone!
milli-Farads (mF) should be used for large values, but the term is generally avoided because of the continued use of the ancient terminology (mainly in the US). When I say ancient, I mean it - these terms date back to the late 1920s or so. Any time you see the term 'mF', it almost certainly means µF - especially if the source is the USA. You may need to determine the correct value from its usage in the circuit.
A capacitor with a value of 100nF may also be written as 0.1µF (especially in the US, but elsewhere as well). A capacitor marked on a schematic as 2n2 has a value of 2.2nF, or 0.0022µF. It may also be written (or marked) as 2,200pF or 222. These are all equivalent, and although this may appear confusing (it is), it is important to understand the different terms that are applied.
MKT and MKP (polyester and polypropylene respectively) 'box' style capacitors as well as many ceramic and SMD (surface mount) capacitors and resistors are marked using a 3 digit code. The first two digits are the value (e.g. 22x or 47x) and the third number is the number of zeros that follow. The value is in picofarads (or ohms for SMD resistors so marked), so 222 means 2200 pF = 2.2nF. Likewise, 475 means 4,700,000pF or 4.7µF. Get used to this code, as it is very common.
A capacitor has an infinite (theoretically!) resistance at DC, and with AC, it has an impedance. Impedance is defined as a non-resistive (or only partially resistive) load, and is frequency dependent. This is a very useful characteristic, and is used to advantage in many circuits. All filters rely on reactive components (capacitors and/ or inductors).
In the case of a capacitor, the impedance is called Capacitive Reactance - generally shown as Xc. The formula for calculating Xc is shown below ...
6.1.1 Xc = 1 / 2π f C Where π is 3.14159..., f is frequency in Hertz, and C is capacitance in Farads
The Transposition Triangle can be used here as well, and simplifies the extraction of the wanted value considerably.
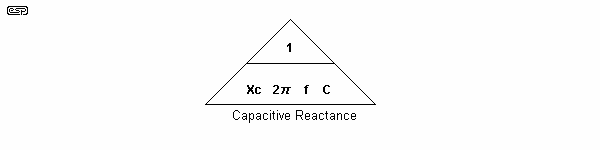
As an example, what is the formula for finding the frequency where a 10µF capacitor has a reactance of 8 Ohms? Simply cover the term 'F' (frequency), and the formula is ...
6.1.2 f = 1 / 2π C Xc
In case you were wondering, the frequency is 1.989kHz (2kHz near enough). At this frequency, if the capacitor were feeding an 8 ohm loudspeaker (a tweeter), the frequency response will be 3dB down at 2kHz, and the signal going to the speaker will increase with increasing frequency. Since the values are the same (8 ohm speaker and 8 ohms reactance) you would expect that the signal should be 6dB down, but because of phase shift (more on this later), it is actually 3dB.
With capacitors, there is no power rating. A capacitor in theory dissipates no power, regardless of the voltage across it or the current through it. In reality, this is not quite true, but for all practical purposes (at audio frequencies!) it does apply. Where very high current is expected (switchmode power supplies for example) there are 'special' capacitors designed to handle high peak current without failure.
Note that even high voltage DC capacitors should never be used across mains AC. There are special capacitors designed for main usage, and they are rated as either 'X' or 'Y' types. Capacitors are also available for use where high frequency pulse current is expected (such as switchmode power supplies). Standard capacitors should not be used at high current!
All capacitors have a voltage rating, and this must not be exceeded. If a higher than rated voltage is applied, the insulation between the 'plates' of the capacitor breaks down, and an arc will often weld the plates together, short circuiting the component. In other cases, the thin metallisation layer will be destroyed around the short, and these caps are sometimes referred to as 'self healing'. The 'working voltage' is DC unless otherwise specified, and application of an equivalent AC signal will probably destroy the capacitor. Some capacitors (notably electrolytic) also have a current rating (ripple current), and if this is exceeded the cap will be damaged. This is especially important with power supplies.
6.1 Standard Values
Capacitors generally follow the E12 sequence, but with some types, there are very few values available within the range. There are also a few oddities, especially with electrolytic caps (these are polarised types).
| 1 | 1.2 | 1.5 | 1.8 | 2.2 | 2.7 | 3.3 | 3.9 | 4.7 | 5.6 | 6.8 | 8.2 | 10 |
Some electrolytic types have non-standard values, such as 4,000µF for example. These are easily recognised, and should cause no fear or panic  .
.
6.2 Capacitor Markings
Unlike resistors, few capacitors are colour coded. Some years ago, various European makers used colour codes, but these have gone by the wayside for nearly all components available today. This is not to say that you won't find them, but I am not going to cover this.
The type of marking depends on the type of capacitor in some cases, and there are several different standards in common use. Because of this, each type shall be covered separately.
6.3 Tolerance
The quoted tolerance of most polyester (or other plastic film types) capacitors is typically 10%, but in practice it is usually better than that. Close tolerance types (e.g. 1%) are available, but they are usually rather expensive. If you have a capacitance meter, it is far cheaper to buy more than you need, and select them yourself.
Electrolytic capacitors have a typical tolerance of +50/-20%, but this varies from one manufacturer to the next. Electrolytics are also affected by age, and as they get older, the capacitance falls. Modern electros are better than the old ones, but they are still potentially unreliable at elevated temperatures or with significant current flow (AC, of course).
Electrolytic capacitors also have a parameter called 'ESR' - equivalent series resistance. This is often quoted in datasheets, and an ESR tester is the quickest way to find out if an electro is on the way out. ESR rises (sometimes quite dramatically) as the capacitor ages, and is a better indicator of impending failure than measuring the capacitance.
6.4 Capacitance Materials
As you have no doubt discovered by now, the range is awesome. Although some of the types listed below are not especially common, these are the most popular of the capacitors available. There is a school of thought that the differences between various dielectrics are audible, and although this may be true in extreme cases, generally I do not believe this to be the case - provided of course that a reasonable comparison is made, using capacitors designed for the application.
Many of the capacitors listed are 'metallised', meaning that instead of using aluminium or other metal plates, the film is coated with an extremely thin layer of vaporised metal. This makes the capacitor much smaller than would otherwise be the case.
This is only a basic listing, but gives the reader an idea of the variety available. The recommendations are mine, but there are many others in the electronics industry who will agree with me (as well as many who will not - such is life).
Apart from the desired quantity of capacitance, capacitors have some unwanted features as well. Most of them have measurable internal inductance (although it's usually very low), and they all posses some value of internal series resistance (although generally small). The resistance is referred to as ESR (Equivalent Series Resistance), and this can have adverse effects at high currents (e.g. power supplies). Although it exists in all capacitors, ESR is generally quoted only for electrolytics. ESL (equivalent series inductance) is rarely provided. ESL usually depends on the physical length of the capacitor, but the length of the leads (or associated printed circuit board tracks) is often dominant.
As noted above, many capacitors use a three digit code for the value (as shown for resistors, above). The value is in picofarads, so a cap marked 224 is 220,000pF, or 220nF. Letters are used to indicate tolerance - 'J' is the most common (5%), followed by 'K' (10%).
These are the last of the purely passive components. An inductor is most commonly a coil, but in reality, even a straight piece of wire has inductance. Winding it into a coil simply concentrates the magnetic field, and increases the inductance considerably for a given length of wire. Although there are some very common inductive components (such as transformers, which are a special case), they are not often used in audio. Small inductors are sometimes used in the output of power amplifiers to prevent instability with capacitive loads.
Note: Transformers are a special case of inductive components, and are covered separately (see Transformers).
Even very short component leads have some inductance, and like capacitance, it is just a part of life. Mostly in audio, these stray inductances cause no problems, but they can make or break a radio frequency circuit, especially at the higher frequencies. A 10mm length of 1mm diameter wire has an inductance of about 6nH, or 105nH for 100mm. This depends on wire size and the proximity of the supply and return wires (where applicable). A handy calculator is available at Research Solutions & Resources LLC. As wire diameter is decreased for a given length, inductance is increased.
An inductor can be considered the opposite of a capacitor. It passes DC with little resistance, but becomes more of an obstacle to the signal as frequency increases.
There are a number of different symbols for inductors, and three of them are shown below. Somewhat perversely perhaps, I use the 'standard' symbol most of the time, since this is what is supported best by my schematic drawing package. I find the 'Euro' version somewhat annoying, as it's not immediately recognised as a coil by many readers.
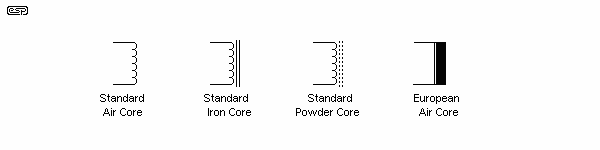
Dotted lines instead of solid mean that the core is ferrite or powdered iron, rather than steel laminations or a toroidal steel core. Note that pure iron is rarely (if ever) used, since there are various grades of steel with much better magnetic properties. The use of a magnetic core further concentrates the magnetic field, and increases inductance, but at the expense of linearity. Steel or ferrite cores should never be used in crossover networks for this reason (although many manufacturers do just that, and use bipolar electrolytic capacitors to save costs).
Inductance is measured in Henrys (H) and has the symbol 'L' (yes, but ... Just accept it  ). The typical range is from a few micro-Henrys up to 10H or more. Although inductors are available as components, there are few (if any) conventions as to values or markings. Some of the available types may follow the E12 range, but then again they may not. The range of inductances is generally far more limited than those for capacitors, but they can be wound for any inductance desired.
). The typical range is from a few micro-Henrys up to 10H or more. Although inductors are available as components, there are few (if any) conventions as to values or markings. Some of the available types may follow the E12 range, but then again they may not. The range of inductances is generally far more limited than those for capacitors, but they can be wound for any inductance desired.
Like a capacitor, an inductor has reactance as well, but it works in the opposite direction. The formula for calculating the inductive reactance (XL) is ...
7.1.1 XL = 2π f L Where L is inductance in Henrys
As before, the transposition triangle helps us to realise the wanted value without having to remember basic algebra.
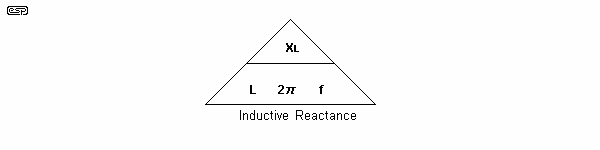
An inductor has a reactance of 8 ohms at 2Khz. What is the inductance? As before, cover the wanted value, in this case inductance. The formula becomes ...
7.1.2 L = XL / 2π f
The answer is 636µH. From this we could deduce that a 636µH inductor in series with an 8 ohm (resistive) loudspeaker will reduce the level by 3dB at 2kHz. Like the capacitor there is phase shift, so when inductive reactance equals resistance, the response is 3dB down, and not 6dB as would be the case with two equal resistances. What we have done in these examples is design a simple 2kHz passive crossover network, using a 10µF capacitor to feed the tweeter, and a 636µH inductor feeding the low frequency driver.
Like a capacitor, an inductor (in theory) dissipates no power, regardless of the voltage across it or the current passing through. In reality, all inductors have resistance, so there is a finite limit to the current before the wire gets so hot that the insulation melts. The parasitic series resistance causes problems with passive crossover networks, but can (sometimes) be used to your advantage.
7.1 Quality Factor
The resistance of a coil determines its Q, or Quality factor. An inductor with high resistance has a low Q, and vice versa. I do not propose to cover this in any more detail at this stage, and most commercially available inductors will have a sufficiently high Q for anything we need in audio. If desired, the Q of any inductor may be reduced by wiring a resistor in series or parallel with the coil, but it cannot be increased because of its internal limitation.
7.2 Power Ratings
Because of the resistance, there is also a limit to the power that any given inductor can handle. In the case of any inductor with a magnetic core, a further (and often overriding) limitation is the maximum magnetic flux density supported by the magnetic material before it saturates. Once saturated, any increase in current causes no additional magnetic field (since the core cannot support any more magnetism), and the inductance falls. This causes gross non-linearities, which can have severe repercussions in some circuits (such as a switchmode power supply).
The core material depends on the application. Laminated steel cores can be used up to around 20kHz or so without excessive losses (e.g. audio transformers), but at higher frequencies, ferrite or powdered iron are more common. Powdered iron cores have lower magnetic permeability and can be used where there is a DC component in the waveform. Other cores (steel or ferrite) require an air-gap to reduce the permeability and prevent saturation. Small-signal transformers for audio may use a higher grade of lamination, often a 'special' nickel-iron alloy such as MuMetal. This material has very high permeability, so a transformer can have high inductance with a small core. These materials are intolerant of DC in the windings.
7.3 Inductance Materials
The most common winding material is copper, and this may be supported on a plastic bobbin, or can be self-supporting with the aid of cable ties, lacquer, or epoxy potting compounds. Iron or ferrite cores may be toroidal (shaped like a ring), or can be in the traditional EI (ee-eye) format. In some cases for crossover networks and some other applications, a piece of magnetic material is inserted through the middle of the coil, but does not make a complete magnetic circuit. This reduces inductance compared to a full core, but reduces the effects of saturation, and allows much higher power ratings. It also adds distortion.
7.4 Core Types
Inductors may use a variety of materials for the core, ranging from air (lowest inductance, but highest linearity), through to various grades of steel or ferrite materials. Since inductors are nearly always used for AC operation, the constantly changing magnetic flux will induce a current into any conductive core material in a similar manner to a transformer. This is called 'eddy current' and represents a total loss in the circuit. Because the currents may be very high, this leads to the core becoming hot, and also reduces performance.
To combat this, steel cores are laminated, using thin sheets of steel insulated from each other. This prevents the circulating currents from becoming excessive, thereby reducing losses considerably. As the frequency increases, even the thin sheets will start to suffer from losses, so powdered iron (a misnomer, since it is more commonly powdered steel) cores are used. Small granules of magnetic material are mixed with a suitable bonding agent, and fired at high temperature to form a ceramic-like material that has excellent magnetic properties. The smaller the magnetic particles (and the less bonding agent used), the better the performance at high power and high frequencies. It is important that the individual granules are insulated from each other, or losses will increase.
These materials are available in a huge variety of different formulations, and are usually optimised for a particular operating frequency range. Some are designed for 20kHz up to 200kHz or so, and these are commonly used for switchmode power supplies, (pre LCD flat screen) television 'flyback' transformers and the like. Other materials are designed to operate at radio frequencies (RF), and these are most commonly classified as 'ferrite' cores. In some cases, the terms 'powdered iron' and 'ferrite' are used interchangeably, but this is not correct - they are different materials with different properties.
These are covered in more detail in the transformers article.
Components in combination form most of the circuits we see. All passives can be arranged in series, parallel, and in any number of different ways to achieve the desired result. Amplification is not possible with passive components, since there is no means to do so. This does not mean that we are limited - there are still many combinations that are extremely useful, and they are often used around active devices (such as opamps) to provide the characteristics we need. Parallel operation is often used to obtain greater power, where a number of low power resistors are wired in parallel to get a lower resistance, but higher power. Series connections are sometimes used to obtain very high values (or to increase the voltage rating). There are endless possibilities, and I shall only concentrate on the most common.
See Section 4.2 above for a couple of alternatives to the 'traditional' reciprocals technique.
8.1 Resistors
Resistors can be wired in parallel or in series, or any combination thereof, so that values greater or smaller than normal or with higher power or voltage can be obtained. This also allows us to create new values, not catered for in the standard values.
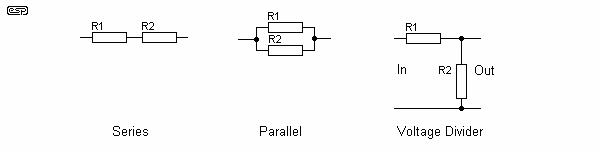
Series: When wired in series, the values simply add together. A 100 ohm and a 2k2 resistor in series will have a value of 2k3.
8.1.1 R = R1 + R2 (+ R3, etc.)
Parallel: In parallel, the value is lower than either of the resistors. A formula is needed to calculate the final value
8.1.2 1/R = ( 1/R1 + 1/R2 (+ 1/R3 etc.)) Also written as ... 8.1.3 R = 1 / (( 1 / R1 ) + ( 1 / R2 )) An alternative for two resistors is ... 8.1.4 R = ( R1 × R2 ) / ( R1 + R2 )
The same resistors as before in parallel will have a total resistance of 95.65 ohms (100 || 2,200). Either formula above may be used for the same result.
Four 100 ohm 10W resistors gives a final value of either 400 ohms 40W (series), 25 ohms 40W (parallel) or 100 ohms 40W (series/ parallel).
Voltage Dividers: One of the most useful and common applications for resistors. A voltage divider is used to reduce the voltage to something more suited to our needs. This connection provides no 'transformation', but is used to match impedances or voltage levels. The formula for a voltage divider is ...
8.1.5 Vd = ( R1 + R2 ) / R2 or ... 8.1.6 Vd = ( R1 / R2 ) + 1
With our standard resistors as used above, we can create a voltage divider of 23 (R1=2k2, R2=100R) or 1.045 (R1=100R, R2=2k2). Perhaps surprisingly, both of these are useful !
8.2 Capacitors
Like resistors, capacitors can also be wired in series, parallel or a combination.
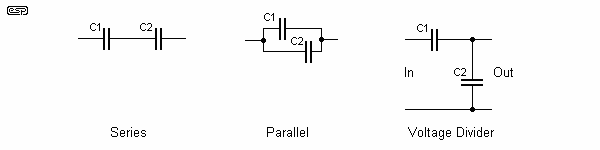
The capacitive voltage divider may come as a surprise, but it is a useful circuit, and is common in RF oscillators and precision attenuators (the latter in conjunction with resistors). Despite what you may intuitively think, the capacitive divider is not frequency dependent, so long as the source impedance is low, and the load impedance is high compared to the capacitive reactance.
When using caps in series or parallel, exactly the opposite formulae are used from those for resistance. Caps in parallel have a value that is the sum of the individual capacitances. Here are the calculations ...
Parallel: A 12nF and a 100nF cap are wired in parallel. The total capacitance is 112nF
8.2.1 C = C1 + C2 (+ C3, etc.)
Series: In series, the value is lower than either of the caps. A formula is needed to calculate the final value.
8.2.2 1 / C = 1/C1 + 1/C2 ( + 1/C3 etc.) Also written as ... 8.2.3 C = 1 / (( 1/C1 ) + ( 1/C2 )) An alternative for two capacitors is ... 8.2.4 C = ( C1 × C2 ) / ( C1 + C2 )
This should look fairly familiar by now. The same two caps in series will give a total value of 10n7 (10.7nF).
The voltage divider is calculated in the same way, except that the terms are reversed (the larger capacitor has a lower reactance). You could be forgiven if you imagine that a capacitive voltage divider will affect the frequency response. It does, but only at low frequencies where the reactance of either capacitor is 'significant' with respect to resistors (or inductors) that may also be part of the circuit. Assuming a zero ohm source and infinite load, two caps act as a voltage divider at any 'sensible' frequency. In this context 'sensible' is determined by the capacitance.
8.2.5 Vd = ( C2 / C1 ) +1
A pair of 100nF capacitors will provide an AC voltage division of two, and if C1 = 10nF and C2 = 100nF, the circuit has an AC voltage division of 11. Capacitive voltage dividers are commonly used in parallel with resistive voltage dividers to ensure extended frequency response in high impedance circuits. See Project 16 (audio millivoltmeter) for an example.
8.3 Inductors
I shall leave it to the reader to determine the formulae, but suffice to say that they behave in the same way as resistors in series and parallel. The formulae are the same, except that 'L' (for inductance) is substituted for 'R'.
An inductive voltage divider can also be made, but it is much more common to use a single winding, and connect a tapping to it for the output. This allows the windings to share a common magnetic field, and makes a thoroughly useful component. These inductors are called 'autotransformers', and they behave very similarly to a conventional transformer, except that only one winding is used, so there is no isolation. As a suitable introduction to the transformer, I have shown the circuit for a variable voltage transformer, called a Variac™ (this is trademarked, but the term has become generic for such devices). Variacs have their own page - see Transformers - The Variac.
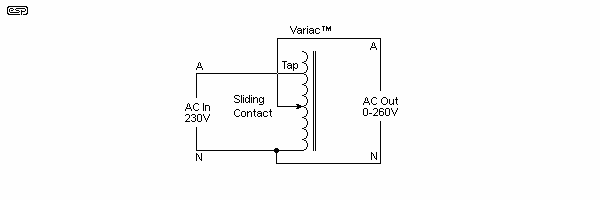
A Variac is nothing more than an iron cored inductor. The mains is applied to a tap about 10-15% from the end of the winding. The sliding contact allows the output voltage to be varied from 0V AC, up to about 260V (for a 230V version). As a testbench tool they are indispensable, and they make a fine example of a tapped inductance (or to be more accurate, a continuously variable autotransformer).
I stated before that passive components cannot amplify, yet I have said here that 230V input can become 260V output. Surely this is amplification? No, it is not. This process is 'transformation', and is quite different. The term 'amplifier' indicates that there will be a power gain in the circuit (as well as voltage gain in most amps), and this cannot be achieved with a transformer. Even assuming an 'ideal' component (i.e. one having no losses), the output power can never exceed the input power, so no amplification has taken place.
When any or all of the above passive components are combined, we create real circuits that can perform functions that are not possible with a single component type. These 'composite' circuits make up the vast majority of all electronics circuits in real life, and understanding how they fit together is very important to your understanding of electronics.
The response of various filters is critical to understanding the way many electronics circuits work. Figure 5.0 shows the two most common, and two others will be introduced as we progress further.
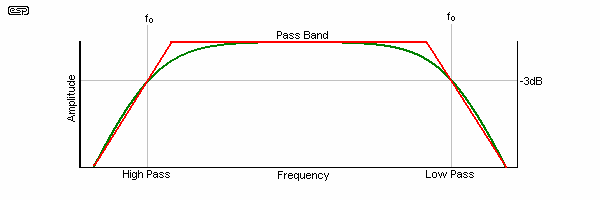
The theoretical response is shown in red, and the actual response is in green. Real circuits (almost) never have sharp transitions, and the curves shown are typical of most filters. The most common use of combined resistance and reactance (using a capacitor, inductor or both) is for filters. fo is the frequency at which response is 3dB down in all such filters.
Within this article, only single pole (also known as 1st order) filters will be covered - the idea is to learn the basics, and not get bogged down in great detail with specific circuit topologies. A simple first order filter has a rolloff of 6dB per octave, meaning that the voltage (or current) of a low pass filter is halved each time the frequency is halved. In the case of a high pass filter, the signal is halved each time the frequency is doubled. These conditions only apply when the applied signal is at least one octave from the filter's 'corner' frequency.
This slope is also referred to as 20dB per decade, so the signal is reduced (asymptotically) by 20dB for each decade (e.g. from 100Hz to 1kHz) from the corner frequency. If you don't know the term, 'asymptotically' means that it approaches the claimed value more closely as you extend towards infinity, but it never actually gets there.
When resistance (R) and capacitance (C) are used together, we can start making some useful circuits. The combination of a non-reactive (resistor) and a reactive (capacitor) component creates a whole new set of circuits. Simple filters are easily made, and basic circuits such as integrators (low pass filters) and differentiators (high pass filters) will be a breeze after this section is completed.
The frequency of any filter is defined as that frequency where the signal is 3dB lower than in the pass band. A low pass filter is any filter that passes frequencies below the 'turnover' point, and the relationship between R, C and F is shown below ...
9.1.1 of = 1 / 2π R C I shall leave it to you to fit this into the transposition triangle.
A 10k resistor and a 100nF capacitor will have a 'transition' frequency (of) of 159Hz, and it does not matter if it is connected as high or low pass. Sometimes, the time constant is used instead - Time Constant is defined as the time taken for the voltage to reach 63.2% of the supply voltage upon application of a DC signal, or discharge to 36.8% of the fully charged voltage upon removal of the DC. This depends on the circuit configuration.
9.1.2 T = R C Where T is time constant
For the same values, the time constant is 1ms (1 millisecond, or 1/1,000 second). The time constant is used mainly where DC is applied to the circuit, and it is used as a simple timer, but is also used with AC in some instances. From this, it is obvious that the frequency is therefore equal to
9.1.3 of = 1 / 2π T
This is not especially common, but you may need it sometime.
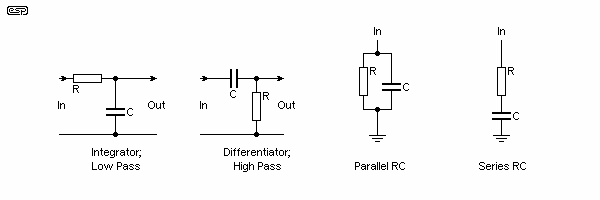
The above are only the most basic of the possibilities, and the formula (9.1.1) above covers them all. The differentiator (or high pass filter) and integrator (low pass filter) are quite possibly the most common circuits in existence, although most of the time you will be quite unaware that this is what you are looking at. The series and parallel circuits are shown with one end connected to earth/ ground - again, although this is a common arrangement, it is by no means the only way these configurations are used. For the following, we shall assume the same resistance and capacitance as shown above - 10k and 100nF.
The parallel RC circuit will exhibit only the resistance at DC, and the impedance will fall as the frequency is increased. At high frequency, the impedance will approach zero Ohms. At some intermediate frequency determined by formula 9.1.1, the reactance of the capacitor will be equal to the resistance, so (logically, one might think), the impedance will be half the resistor value. In fact, this is not the case, and the impedance will be 7k07 Ohms. This needs some further investigation ...
The series RC circuit also exhibits frequency dependent behaviour, but at DC the impedance is infinite (for practical purposes), and at some high frequency it is approximately equal to the resistance value alone. It is the opposite of the parallel circuit. This circuit is seen at the output of almost every solid state amplifier ever made, and is intended to stabilise the amplifier at high frequencies in the presence of inductive loads (speaker cables and loudspeakers).
Because of a phenomenon called 'phase shift' (see below) these RC circuits can only be calculated using vector mathematics (trigonometry) or 'complex' arithmetic, neither is particularly straightforward, and I will look at a simple example only - otherwise they will not be covered here.
9.1.4 Z = √ (1 / ( 1 / R² + 1 / Xc² )) For parallel circuits, or ... 9.1.5 Z = √ ( R² + Xc² ) For series circuits.
Simple !!! Actually, it is. In the case of the series circuit, we take the square root of the two values squared - those who still recall a little trigonometry will recognise the formula ...
The square on the hypotenuse is equal to the sum of the squares of the other two sides - it's the old 'right-angled triangle' formula
It is a little more complex for the parallel circuit, just as it was for parallel resistors - the only difference is the units are squared before we add them, take the square root, and the reciprocal. If this is all too hard, there is a simple way, but it only works when the capacitive reactance equals resistance. Since this is the -3dB frequency (upon which nearly all filters and such are specified), it will suit you most of the time.
9.1.6 Z = 0.707 × R For parallel circuits, and ... 9.1.7 Z = 1.414 × R For series circuits.
If we work this out - having first calculated the frequency where Xc = R (159Hz), we can now apply the maths. Z is equal to 7k07 for the parallel circuit, and 14k1 for the series circuit. Remember, this simple formula only applies when Xc = R.
Figure 5.2 shows one of the effects of phase shift in a capacitor - the current (green trace) is out of phase with respect to the voltage (red trace). In fact, the current is leading the voltage by 90 degrees. It may seem impossible for the current through a device to occur before the voltage, and this situation only really applies to 'steady state' signals. This is known in electrical engineering as a leading power factor.
However baffling this might seem, it must be understood that the effect is quite real, and the current really does occur before the voltage. I know this is confusing and seemingly impossible, but it is true whether you choose to accept it or not.
It becomes more complex mathematically to calculate the transient (or varying signal) behaviour of the circuit, but interestingly, this usually has no effect on sound, and the performance with music will be in accordance with the steady state calculations.
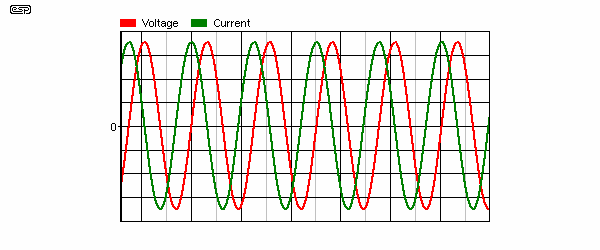
The phase shift through any RC circuit varies with frequency, and at frequencies where Xc is low compared to the -3dB frequency, it is minimal. Static phase shift is not audible in any normal audio circuit, but it is audible if one signal has phase shift, the other does not, and they are summed electrically or acoustically.
When the value of the integration or differentiation capacitor is large compared to the lowest operating frequency, it is more commonly called a coupling capacitor. The same formulae are used regardless of the nomenclature of the circuit.
The combination of resistance (R) and inductance (L) is much less common than RC circuits in modern electronics circuits. Many of the same circuit arrangements can be applied, but it uncommon to do so.
These days, the most common application of RL circuits is in passive crossover networks. The speaker is not pure resistance, but is often compensated with a 'Zobel' network in an attempt to cancel the inductive component of the speaker.
The turnover frequency (-3dB) is determined by the formula below.
9.2.1 of = R / 2π L Again, I shall leave it to you to fit this into the transposition triangle
A couple of simple RL filters are shown in Figure 9.4 for reference. These are not uncommon circuits, and they may be seen in amplifiers and loudspeaker crossovers networks almost anywhere.
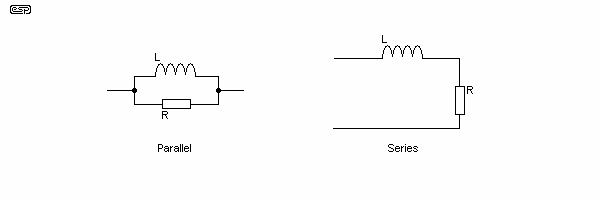
The series circuit is typical of a simple crossover network to a woofer, and the 'resistance' is the loudspeaker. The parallel circuit is seen on the output of many amplifier circuits, and is used to isolate the amplifier from capacitive loading effects at high frequencies. Because of the phase shift introduced by capacitance, some amplifiers become unstable at very high frequencies, and tend to oscillate. This affects sound quality and component life (especially the transistors), and is to be avoided.
Inductors (like capacitors) are reactive, and they cannot be calculated simply. To determine the impedance of a series or parallel circuit requires exactly the same processes as described for capacitors. Like capacitors, inductors cause phase shift, except the shift is the reverse - the current occurs after the voltage. In electrical engineering, this is referred to as a lagging power factor. This is shown in Figure 9.4, and again, the green trace is current - it can be seen that the current occurs after the voltage.
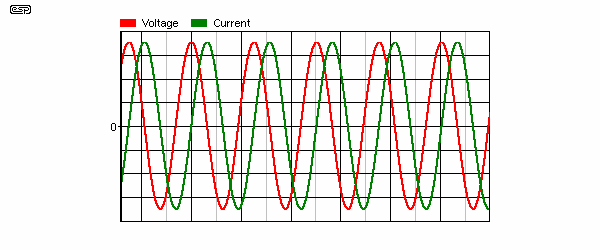
Just as we did with capacitive reactance, if we work only with the -3dB frequency, this is where inductive reactance (XL) and resistance are equal. Because the inductive reactance increases with increasing frequency (as opposed to capacitive reactance which falls as frequency increases), the configurations for low pass and high pass are reversed. We can still use the same simple formulae, and again, these only work when XL is equal to R.
9.2.2 Z = 0.707 × R For parallel circuits, and ...
9.2.3 Z = 1.414 × R For series circuits.
Integrators and differentiators can also be made using RL circuits, but they are very uncommon in normal linear electronics circuits and will not be covered at this time.
The combination of capacitance and inductance (at least in its 'normal' form) is quite uncommon in audio or other low frequency circuits. Simulated inductors (using an opamp to create an artificial component with the properties of an inductor) are common, and they behave in a very similar manner in simple circuits.
The combination using real inductors has some fascinating properties, depending on the way they are connected. These will be covered only briefly here - they are much more commonly used in RF work, and in some cases for generation of very high voltages for experimental purposes (Tesla coils and car ignition coils spring to mind). A series resonant circuit can generate voltages that are many times the input voltage, and this interesting fact can be used to advantage (or to kill yourself!).
An inductor and capacitor in series presents a very low impedance at resonance, defined as the frequency where inductive and capacitive reactance are equal. With ideal (i.e. completely lossless) components, the impedance at resonance is zero, but in reality there will always be some resistance because of the resistance of the coil, and some small capacitive losses.
Resonance (of) is determined by the formula shown as 9.3.1, and you can extract L and C as well ...
9.3.1 of = 1 / 2π × √ L C
9.3.2 L = 1 / (4 × π² × of² × C )
9.3.2 C = 1 / (4 × π² × of² × L )
To use the transposition triangle, you need a hint - to extract L or C, all other terms must be squared first. (For example, 1 = 4 π ² f ² L C - the triangle is very easy now !) While I have saved you the trouble, it's instructive for you to work it out yourself. For reasons that I can't quite fathom, if you look for the LC resonance formulae online, almost no-one shows the derived versions that let you extract L or C based on the resonant frequency. This is a shame, because they can be very useful.
Parallel resonance uses the same formula, and at resonance the impedance is theoretically infinite with ideal components. Both of these combinations are used extensively in radio work, and parallel resonance circuits are also used in tape recorders, for example. They were once used as the filters for graphic equalisers, but electronic filters are cheaper, more flexible and do not pick up hum fields from nearby transformers.
It is somewhat beyond the scope of this article to describe the use of tuned circuits in tape recorders in detail, but they use a high frequency bias oscillator to overcome the inherent distortion that occurs when a material is magnetised. The HF signal is at a very high amplitude, because the inductance of the tape heads causes their impedance to be very high at the bias frequency (typically between 50kHz and 150kHz). Should this high amplitude high frequency be fed into the record amplifier, the low impedance of the amp circuit will 'steal' most of the bias, the amplifier will probably be forced into distortion as well, and the circuit won't work. A parallel resonant circuit tuned to the bias frequency is used to isolate the bias from the amp. It has no effect on the audio signal because the resonance is very sharp, and it presents a low impedance path for all signals other than the high frequency bias voltage.
A parallel or series resonant circuit can be indistinguishable from each other in some circuits, and in RF work these resonant systems are often referred to as a 'tank' circuit. Energy is stored by both reactances, and is released into a load (such as an antenna). The energy storage allows an RF circuit to oscillate happily with only the occasional 'nudge' from a transistor or other active device - this is usually done once each complete cycle.
In the two circuits below, I used 10mH and 100µF as the reactive components. The tuning frequency is 159Hz - use the formula shown above to verify this. At the resonant frequency, the capacitor has a reactance of 10 ohms, as does the inductor. When both capacitive and inductive reactance are equal, the circuit is tuned and is purely resistive - the equal and opposite reactances cancel. A parallel tuned LC circuit is an open circuit at resonance, and series tuned circuits are a short (ignoring stray resistance in the coils and ESR in the capacitors).
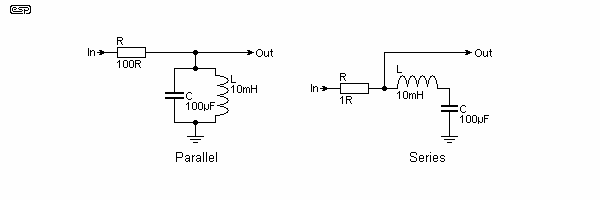
I have shown the series circuit with an input and an output. If the inductance and capacitance were to be selected for resonance at the mains frequency, and a low voltage / high current transformer were used to supply a voltage at the input of the circuit, the voltage across the capacitor could easily reach several thousand volts. Exactly the same voltage would appear across the inductor, but the two voltages are equal and opposite, so they cancel out. The result is that at resonance, the series LC network appears to be a short circuit. The only remaining impedance is the resistance of the wire used in the coil, and a small amount of ESR (equivalent series resistance) in the capacitor.
Warning
Do not attempt to build a series resonant circuit for use with mains voltages and frequency, as serious injury or death may occur. The circuit is potentially lethal, even with an input of only a few volts.
The supply current will also be extremely high, as the series resonant circuit behaves like a short circuit at resonance. This is not in jest !
In all cases when the circuit is at resonance, the reactance of the capacitor and inductor cancel. For series resonance, they cancel such that the circuit appears electrically as almost a short circuit. Parallel resonance is almost an open circuit at resonance. Any 'stray' impedance is pure resistance for a tank circuit at resonance.
The frequency response of the LC tuned circuits shown in Figure 9.5 is either a frequency peak (typically using parallel resonance) or dip (series resonance) as shown in Figure 9.6. fo is now the resonant frequency (the term seems to have come from RF circuits, where fo means frequency of oscillation).
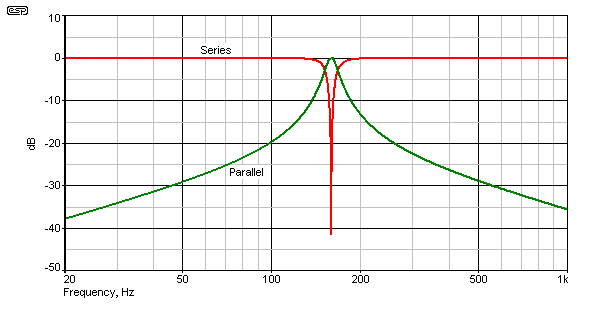
The 'Q' (or 'Quality factor') of these circuits is very high, and the steep slopes leading to and from fo are quite visible - particularly with the series resonant notch filter. Ultimately, a frequency is reached where either the inductance or capacitance becomes negligible compared to the other, and the slope becomes 6dB per octave, as with any other single pole filter. Multiple circuits can be cascaded to improve the ultimate rolloff.
Q is defined as the frequency divided by the bandwidth, measured from the 3dB points relative to the maximum or minimum response, FL and FH. For example, the filters shown above have a centre frequency (fo) of 159Hz, and for the bandpass filter the -3dB frequencies are 151.4Hz and 167.2Hz. 159Hz divided by the difference (15.8Hz) gives a Q of 10.06 - there are no units for Q, it is a relative measurement only.
These figures were obtained using the circuits shown in Figure 9.5, with all values as shown in the circuits. In a simulation with the series resonant circuit, I used an input voltage of 10V (10V through a 1 ohm resistor causes 10A to flow) at 159Hz, and the voltage across L and C is almost 100V, but can be far greater if the series resistance is lower. This is not amplification, since there is no power gain, but even at low input voltages, the circuit can be potentially deadly - especially when driven from a low source impedance. Needless to say, the capacitor and inductor must be rated for the voltage, and this rating is AC - a DC capacitor will fail with high voltage AC applied.
A bandpass filter using parallel resonance may be used to filter a specific frequency, and effectively removes all others. This is not strictly true of course, since the rolloff slopes are finite, but the other (unwanted) frequencies will be suppressed by 20dB at a little more than ½ octave either side of the centre frequency (98Hz on the low side and 257Hz on the high side to be exact). As the input resistance is increased, so too is the Q of the filter, provided that coil resistance is minimal. In a simulation where the 100 ohm resistor was increased to 1k, the Q rises to 100 - the 3dB bandwidth is only 1.59Hz wide! However, just 1 ohm of coil resistance is enough to reduce the Q to only 9. Low loss components are essential for good performance with all LC resonant circuits.
Likewise, a bandstop filter (such as the series resonance circuit shown) will remove an offending frequency, but allows everything else through. Quite obviously, it's not always as simple as that, but the principle is sufficiently sound that these LC circuits are used in radio and TV receivers to extract the wanted station and reject the others quite effectively - although generally with some help from a lot of other circuitry as well. In the early days of AM radio, many people used crystal sets that had a single tuning coil and capacitor. Tuned circuits are also used in tape recorders, both to generate the bias frequency and prevent it from overloading the tape-head drive amplifier. The applications for tuned circuits are so vast that they warrant large sections of reference books, which have indeed been written.
While modern ICs and other components (such as crystals and ceramic filters) have reduced the need for LC tuned circuits, they are still used extensively in many areas of electronics, including RF (radio frequency) circuits and passive loudspeaker crossover networks. While not normally considered to be 'tuned circuits', they most certainly are. They are heavily damped by the connected speaker drivers in normal use, so are commonly seen as simple filters. Just don't mess with a passive crossover using coils and caps without the drivers connected, as bad things can happen!
Despite their apparent simplicity, LC filters can be difficult to design well and require considerable skill if high Q circuits are needed or when they are used as speaker crossovers.
This is the first part of a two-part article to help newcomers to the fascinating world of electronics, concentrating on passive components. It is by no means complete, but will hopefully assist you greatly in understanding the basic concepts. There are many more articles that cover more complex areas as well, including opamps, transistors and even valves (vacuum tubes). The latter are in their own section - see the Valve Info Index for more info.
Should you want to know more (and there is so much more!), there are many books available designed for the technical and trades courses at universities and colleges. These are usually the best at describing in great detail each and every aspect of electronics, but quite often provide far more information than you really need to understand the topic.
This series of articles is designed to hit the middle ground, not so much information as to cause 'brain pain', but not so little that you are left oblivious to the finer points. I hope I have succeeded so far.
One of the most difficult things for beginners and even professionals to understand is why there are so many of everything - capacitors, inductors and (especially?) resistors, ICs and transistors - the list is endless. Surely it can't be that hard? The economy of scale alone would make consolidation worthwhile. Unfortunately, this isn't really an option, and the number of different parts that exist are determined largely by market forces. If enough people want something, then it's almost certain that someone will make it available.
Phil Allison, a contributor to The Audio Pages, suggests an explanation for some of the dilemmas that the beginner faces ...
Passive electronic components exist in theory only. They are mathematical inventions that obey laws specified in formulae like Ohms Law and the equations that define them.
Physical objects can be constructed that can mimic these equations with varying degrees of accuracy and within the limits of voltage, current and power (or heat) that causes minimal damage to the materials they are made from. No perfect passive components exist because all passive components have resistance, capacitance and inductance as the laws of nature require.
Capacitors are so called because they possess more capacitance than resistance or inductance and the same remark goes for resistors and inductors.
A large industry exists to design and manufacture components for the production of consumer electronics like TV sets and other home entertainment. Also, a smaller industry exists making specialist products for industrial, professional and military electronics. There is a lot of money invested in component making as nothing electronic can be built without them. It is also a very competitive business with many players.
Now, the vast majority of electronics designers do not concern themselves with active or passive component design unless of course they work for one of the component makers. They take their various offerings like manna from heaven and attempt to produce devices for people to use. It is important for a designer to know the characteristics and limitations of each product a component maker is offering in order to use them successfully and efficiently in terms of cost. As a result, every piece of electronic design is full of compromises due to many imperfections in every component.
There are numerous types of component because the business end of electronics is making practical things at the lowest possible cost. This fact explains the many different offerings at various prices and levels of performance. Horses for courses.
It also explains why electronic things fail or break down. Most are built using the fewest and cheapest components that will do the job for just a few years. Passive and active component makers work to this standard for all consumer oriented products. Maybe they should put a 'use by' date on each one :-).
Specialist grade electronic components built for a long life and high reliability cost 10 to 100 times more than normal grade and are bought only by the likes of NASA and suppliers to the military and/or scientific community (where cost is still important, but failure is likely to cost a great deal more !)
I do hope this is not too iconoclastic* for novices to the art.
No, Phil - I for one don't think this is iconoclastic in the least - although there are many 'golden ear' types who will disagree. I believe this to be a fair and reasonable comment on the 'state of the art', and is extremely well put as well  . All in all, this makes a fine conclusion to Part 1.
. All in all, this makes a fine conclusion to Part 1.
* Iconoclastic - from iconoclast; one who breaks images or destroys the cherished beliefs of others.
 Main Index Main Index
 Articles Index Articles Index
|