
 |
| Elliott Sound Products | Ohm's Law |
 Main Index Main Index  Articles Index Articles Index |
Ohm's law is one of the first things that anyone learning electronics is taught. It's invariably treated as a simple equation (e.g. R = V / I) without caveats or 'preconditions'. We use it almost every day that we do anything involving electronics or power distribution because it tells us so many things about the circuit being analysed. We take resistance measurements taken with a multimeter as being a true representation of the resistance with the test conditions usually being ignored. Occasionally we might verify the test current or open-circuit voltage used by a multimeter, but most people will never have bothered to do so. This isn't an issue with 99% of the tests we perform.
There is now an 'alternative' explanation of Ohm's law that claims that it relies on the resistance remaining constant at any voltage or current. This distinction was never taught to anyone who studied electronics, and the advent of 'AS' (artificial stupidity) has now managed to convince a number of people that nonlinear resistances (thermistors, incandescent lamps and even some heating appliances) mean that somehow Ohm's law is wrong.
It's been suggested that it should be renamed to 'Ohm's Approximation', something that is bound to seriously annoy anyone who has worked with electronics all their working life. Yes, that includes me. This 'new' explanation is just drivel, and there are countless places in electronics where we calculate the resistance based on the applied voltage and current flow. This works with any resistance material, and it's even applied to zener diodes (to calculate dynamic resistance/ impedance), and it can be used to plot the curve of devices that are often considered to be 'non-ohmic'.
For example, some devices exhibit a negative resistance, at least over part of their operating range. This might sound like a bizarre concept, but it's been explained elsewhere on the ESP site. Negative resistance can be used to drive signal transformers to improve their performance, but it's also a characteristic of arc lamps (e.g. fluorescent lamps) and MOVs (metal oxide varistors.
Note that the term 'impedance' is often used when discussing dynamic resistance (i.e. resistance that changes depending on current), but if the test is done with DC, it really is resistance. The term 'impedance' is usually reserved for AC circuits containing reactive elements (inductors and/ or capacitors).
'Sensible' websites will simply point out the obvious - a light bulb is nonlinear, and will use one as an example of Ohm's law in action. This is expanded below (Section 3), and it shows how Ohm's law can be used to characterise 'weird' behaviour rather than to use it to 'prove' that Ohm's law doesn't apply. Of course it applies, and when used properly (and sensibly) you'll learn far more than you ever will by asking an AI site the question.
Ohm's law should be familiar to anyone involved in electrical devices, and it's not limited to electronics. It's an important part of power distribution, and it applies to any circuit or wiring scheme regardless of the power level involved. If the current through a conductor is measured, the voltage across that conductor is proportional to its resistance. Traditionally, the term 'E' (for electromotive force) was used, but the letter 'V' (for volts) is now far more common.
Expressed in its basic form, Ohm's law simply states that ....
V = I × R
There is absolutely nothing ambiguous, and it doesn't matter if the conductor changes its resistance or not, provided we take a measurement when the current has stabilised. It's been claimed that (somehow) Ohm's law only applies when the resistance is constant. This is just bullshit! The resistance you calculate is the true resistance for the voltage and current applied. It doesn't matter if the resistance you measure with a different voltage is different from that for the initial test. If I apply 1V and measure 1A, the resistance is 1Ω. Just because I increase the voltage to 10V and the current measures 5A does not mean that Ohm's law doesn't apply; it simply means that the resistance has increased, and the actual resistance is now 2Ω with 10V applied. This isn't some strange approximation or a mis-use of Ohm's law, it is Ohm's law.
Ohm's law states that the voltage across a conductor is directly proportional to the current flowing through it, provided all physical conditions and temperatures remain constant ¹. This can also be rephrased ... Ohm's law states that the electric current through a conductor between two points is directly proportional to the voltage across the two points ². This can be expressed as ...
I = V / R or
R = V / I
In Georg Ohm's original claim there is an expectation that the values are constant - for the duration of the measurement (not stated, but implied by just thinking about it for a moment) Primarily, it covers proportionality. Each value is proportional to the others. If you were foolish enough to note a measurement before the meter has stabilised then your reading is meaningless, it's not an indication that Ohm's law doesn't apply! If you do measure a light bulb's resistance, the current from the ohmmeter will already have raised the temperature of the filament, so to get an accurate reading of the resistance at ambient temperature, the current must be as low as possible.
If a meter supplies a current of (say) 10mA to the filament, that will be enough to raise its temperature. But by how much? You need Ohm's law to determine that, using the lowest practicable current (perhaps 100μA, for a filament dissipation of 650nW (assuming a 'cold' resistance of 65Ω). The voltage across the filament will be only 6.5mV, so an accurate meter that can measure that is needed. All of these measurements rely on simple formulae, including Ohm's law.
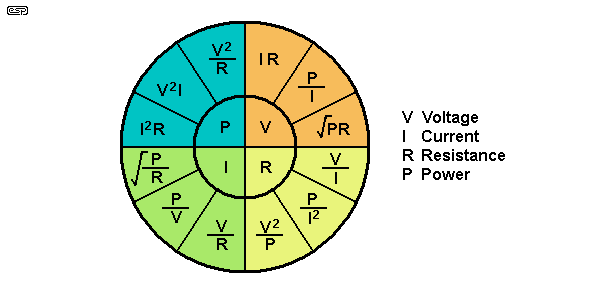
The image shown contains all of the basic calculations you'll use with Ohm's law. Power is included because it's essential that we know how much power a resistor will dissipate under the test conditions that apply for any given Ohm's law calculation. These formulae apply equally to DC and AC, provided that the resistance is not 'contaminated' by inductance or capacitance. All measurements will be contaminated to some degree, but for audio frequencies the normal amount of stray inductance or capacitance is usually not a major source of errors. Normal resistor tolerances will almost always be far greater than any error created by stray impedances.
I asked ChatCPT "Do light bulbs follow Ohm's law?". I got the following 'explanation' ...
Light bulbs can follow Ohm's Law, but not always — it depends on the type of bulb and the conditions under which it's operating.
1. Ohm's Law Recap
Ohm's Law states:
V = I R
where:
V = voltage
I = current
R = resistanceOhm's Law assumes constant resistance — in other words, the component behaves as a linear resistor.
2. Incandescent Bulbs (Do Not Strictly Follow Ohm's Law)
Why? The filament (usually tungsten) heats up significantly when current flows through it.
As the temperature increases, the resistance increases.
This means the relationship between voltage and current is non-linear — so Ohm's Law doesn’t strictly apply.
Resistance is not constant.
In practical terms, an incandescent bulb draws more current when cold and less current as it heats up.3. LEDs and Other Non-Linear Devices (Definitely Do Not Follow Ohm's Law)
LEDs are non-ohmic devices.
Their voltage-current relationship is non-linear and directional (they only conduct in one direction).
They operate based on semiconductor physics, not simple resistance.4. Resistive Heating Elements (Close to Ohm's Law)
Some specialized bulbs or heating elements are designed to have more stable resistance over temperature.
These may more closely follow Ohm's Law, especially over narrow temperature ranges.Summary:
Bulb Type Follows Ohm's Law? Notes Incandescent No (Not exactly) Resistance changes with temperature LED No Strongly non-linear, directional Halogen No (similar to incandescent) Higher-temp, still non-linear Fluorescent/CFL No Uses gas discharge and ballasts Resistive heater Approx. Yes If temp doesn’t change much
This 'explanation' is wrong at so many levels that I don't know where to start. We can start with the definition of Ohm's law, as this is where the confusion starts. The way Ohm's law is written influences how we look at the problem, but in reality that is immaterial. We need to be sensible, or (dare I say it), have a rational approach.
One page I saw claimed that LED 'light bulbs' follow Ohm's law more closely than an incandescent light. This is a pretty clear indication that AS AI was used, because it's hopelessly wrong.
It's quite obvious that, at first glance, the AI explanation seems to make sense. However, it's wrong. Would anyone argue that a pot (potentiometer) is not ohmic? I certainly hope not! Likewise, it would be non-sensible in the extreme to argue that a 1Ω, 1W resistor doesn't follow Ohm's law because it reads open circuit when supplied with 100V. It will blow up, but that doesn't mean that it doesn't follow the law. At an applied voltage of 100V, we might measure 50nA (nanoamps of leakage), so the resistance is 2GΩ. It probably won't be stable though, but when a measurement is taken the resistance (at that time) is correct.
It's a fact of life that materials change their resistance depending on temperature. At 0K (zero Kelvin), most common conductors have very low resistance (some become superconductors), so if we believe AI, nothing follows Ohm's law. In reality, we use the measured resistance of components to determine the temperature (e.g. thermistors), usually by supplying a (reasonably) constant current and measuring the voltage across the thermistor. Ohmmeters measure resistance by using the same principle, and to claim that the resistance must be constant (over an extended range) is obviously stupid.
Unfortunately, there are now countless posts in forum sites (and even some 'scientific' websites) where the AI version is taken as gospel. As I stated in the introduction, this is bullshit. Based on this insanity, nothing follows Ohm's law, because there is no material known that has a zero temperature coefficient of resistance. Likewise, there is no material that can handle the implied infinite change of voltage and current.
All materials that we use (including for resistors) have both a temperature coefficient of resistance and a maximum operating temperature. The reliance on AI to provide usable (and correct) information is highly questionable, as this example exemplifies. The factual pollution that's invading the Interwebs is largely due to people relying on AI to answer questions, and the answers are accepted without a second thought. Expect this to get worse, because many AI systems will reinforce their (wrong) answers by gathering information from external sources. The more often they find the same answer, the greater its 'weight' (i.e. it's assumed to be more factual because it's repeated). This is pure folly, and is the reason that there are so many myths circulating - people make the same assumption.
Ohm's law has sometimes been stated as, "for a conductor in a given state, the electromotive force is proportional to the current produced. "That is, that the resistance, the ratio of the applied electromotive force (or voltage) to the current, "does not vary with the current strength." The qualifier "in a given state" is usually interpreted as meaning "at a constant temperature", since the resistivity of materials is usually temperature dependent. ²
The statement above can be expanded - a "given state" can simply mean that the state remains constant for the duration of the measurement. Taking this to an extreme, we can measure 'dynamic resistance', something that's quoted in many zener diode datasheets. We actually do much the same when measuring a thermistor (or a light bulb), and we can use the following formula ...
ΔR = ΔV / ΔI
The term Δ (delta) simply means 'change of', so we measure a change of voltage and the corresponding change of current, and determine the change of resistance. So, if we were to change the current by 50mA (e.g. from 100mA to 150mA) and we see the voltage change by 100mV (e.g. from 10.0V to 10.1V), the change of resistance is 2Ω. To avoid possible confusion, the dynamic resistance is commonly defined as dynamic impedance, but with a zener diode it really is dynamic resistance - it's not frequency dependent, but measurements are (nearly) always performed using DC. For the voltages and currents used in this example, we'd be looking at a 2W zener diode.
For our light bulb, a 60W, 230V lamp will draw 260.8mA, indicating a resistance of 882Ω. Just because an ohmmeter tells me that the resistance is 69.8Ω doesn't mean that Ohm's law is 'broken'. It tells me that the resistance of the lamp changes as the filament heats up, something that most people involved with electronics already know. We can even use the change of resistance to determine the operating temperature of the filament!
T = ( T0 + ΔR ) / ( α × R0 ) Where
T0 is ambient, T is final temp (°C), ΔR is resistance change and R0 is initial resistance at ambient. α is the thermal coefficient of resistance for tungsten - 0.0045/ °C (4.5 × 10-3).
The answer is 2,600°C or 2,873K - the approximate colour temperature of a 'typical' incandescent lamp (often approximated to 2,700 and called 'warm white' for LED lamps). In all such cases, we measure temperature rise, i.e. the increase above ambient. That's why the formula includes the T0 (ambient) term, as that's added to the temperature rise to get the final temperature.
This is Ohm's law at work. Without it, we'd be in a great deal of trouble. So yes, an incandescent lamp does follow Ohm's law! As for LEDs, they are not resistive per se, but they do have a dynamic resistance/ impedance that can be determined in the same way as the dynamic impedance of a zener diode. The same applies to rectifier diodes and transistor junctions. With semiconductors, matters are complicated a little because silicon has a negative thermal coefficient of resistance (nominally about 70mΩ/ °C or -70×10-3). This (roughly) translates to around -2mV/ °C at normal operating currents for the device.
I consider the AI generated explanation to be specious - it looks plausible, but the one shown (along with many similar) is basically wrong. We use Ohm's law all the time without making any distinction of anything being 'constant'. Circuit simulators treat all resistors as being constant (unless the model is changed to emulate nonlinearity). Using the AI description and examples, all we get is confusion, with no additional clarity and no information that will help anyone.
Using the same technique as described above (for a light bulb), we can also determine the winding temperature of a transformer or loudspeaker voicecoil. The only change is the thermal coefficient of resistance, and (of course) the final temperature. The tempco of copper is 3.93mΩ/ °C (3.93 × 10 -3), and by measuring the resistance we can determine the temperature. This is particularly useful when there is no direct access to the object being measured. It's not hard for a voicecoil to almost double its datasheet value for RE (electrical resistance) if it's pushed hard enough! An example is worthwhile ... you measure the voicecoil resistance at 6Ω at an ambient temperature of 20°C. After running the speaker hard for a few minutes, you take another measurement (which must be done very quickly) and get a new resistance of 9Ω. The voicecoil temperature is therefore ...
T = ( T0 + ΔR ) / ( α × R0 )
T = ( 20 + ( 9 - 6 )) / ( 0.00393 × 6 ) = 147°C
The process described is shown on many websites (including the ESP site), and is a well established technique. As noted already, it uses Ohm's law and a bit of basic maths to determine the temperature. If we were silly enough to believe the premise of the AI description, then we'd be confused, baffled and unable to decide what to do or how to do it.
Whether or not Ohm's law fits an unnecessarily (and pointlessly) strict 'interpretation' is of no consequence. It's still Ohm's law, and it uses the same formulae. Even devices with a negative coefficient of resistance can be measured, so that means you can determine the negative resistance/ impedance of an arc, a neon indicator lamp or (albeit with some difficulty) a semiconductor such as a diac.
Take inspiration from AI at your peril. It can potentially be useful for some mundane tasks, but allowing the output of ChatGPT (or any other AI system) to reinterpret common electrical/ electronic laws or rules is going to lead to tears at the end of the day. Unfortunately, we can only expect this to get worse. 
It's notable that test equipment suppliers ³ don't make silly pronouncements about the applicability or otherwise of Ohm's law when discussing resistance measurement. Meters tell you the actual resistance of the device under test, with the test conditions provided by the meter. If you change the test conditions you may get a different answer, but that does not invalidate the basic principles.
Finally, I'll make the point that none of the articles on the ESP site are written by AI. There is one other example where AI was used as a test (Lock-in Amplifiers - Sub Page) and while the answer wasn't wrong it was essentially useless. Another article shows some pseudo-code generated by ChatGPT, and it's equally as unimpressive. We are starting to see more and more 'blogs' that are fairly obviously created using AI, so the scope for more disinformation grows. While some of it may not be wrong, unless you understand the principles behind the text of the article/ blog/ whatever, you won't know if it is wrong, so nonsense will be propagated across the Net until facts become obscured by 'alternative facts' (which are lies). There is no such thing as an 'alternative fact', something is a fact (i.e. demonstratively correct) or it's not; there is no in-between.
You may hear claims similar to "I saw in on 15 websites, so it must be correct." Not so - the 15 websites you looked at may all have been wrong! Obviously, there are also many things that are right repeated countless times, and the new question is "How do I pick which info is right and which is wrong." Experience helps, but beginners don't have that experience, so can easily be lead astray. Unfortunately, there's no easy answer.
There's probably little doubt that AI (at least the types we mortals have access to) may help us with a lot of basic tasks, but unless the systems are properly trained and mis/ disinformation weeded out we may find ourselves with nowhere to go to get decent information about how things work. If you haven't done so, I encourage the reader to ask an AI system a question to which you know the answer. If the result disagrees with what you know, then it's almost certain that artificial stupidity is hard at work. This isn't going away, so you need to be prepared to be subjected to a lot of nonsense.
 Main Index Main Index  Articles Index Articles Index |