

|
| Elliott Sound Products | Power Amplifier Design Guidelines |
 Main Index
Main Index
 Articles Index
Articles Index
I am amazed at the number of amplifier designers who have, for one reason or another, failed to take some of the well known basics and pitfalls of amp design into consideration during the design phase. While some of these errors (whether of judgement or through ignorance is uncertain) are of no great consequence, others can lead to the slow but sure or instantaneous destruction of an amplifier's output devices.
When I say 'of no great consequence', this is possibly contentious, since a dramatic increase in distortion is hardly that, however in this context it will at least not destroy anything - other than the listener's enjoyment.
Even well known and respected designs can fall foul of some basic errors - this is naturally ignoring the multitude of 'off the wall' designs (e.g. Single-ended MOSFETs without feedback (yecch! - 5% distortion, phtooey), transformer-coupled monstrosities, amplifiers so complex and bizarre that they defy logic or description, etc). This is not including valve amps, these are a 'special' case and in many areas, such as guitar amps, as far as many players are concerned they remain unsurpassed.
In this article, I have attempted to cover some of the areas which require their own special consideration, and the references quoted at the end are excellent sources of more detailed information on the items where a reference is given.
Reference Amplifier
My reference amplifier is shown in Project 3A, and is a hard act to follow. As I have been refining these pages and experimenting with simulations and real life, I have found that this amp is exemplary. It does need a comparatively high quiescent current to keep the output devices well away from crossover distortion, but this is easily accommodated by using decent heatsinks. Even a Class-A system (Death of Zen) fails to come close at medium power, and is barely better at low power.
This amp uses the following ...
It is stable with all conventional loads, capable of 80W into 8 Ohms, and simple to build. Using only commonly available parts, it is also very inexpensive. The amp was designed specifically for DIY, and it is remarkably tolerant of different transistors throughout. This was considered important because there's no point publishing a design that requires exact semiconductors, as output devices (in particular) come and go - what's available today may be very different from what's available in a year, or what was available several years ago.
Note:
This article is not intended to be the 'designers' handbook', but is a collection of notes and ideas showing the influences of the various stages in a typical amplifier. Although I have made suggestions that various topologies are superior to others, this does not mean to imply that they should automatically be used. If one were to combine all the 'best' configurations into a single amp, this is no guarantee that it will perform or sound any better than one using 'lesser' building blocks.
There is a school of thought that the fewer active devices one uses, the better an amp will sound. I do not believe this to be the case, but my own design philosophy is to make any given design as simple as possible, consistent with the level of performance expected of it.
Additional schools of thought will make all manner of claims regarding esoteric components, 'unexplained' phenomena, or will imply that most amplifiers as we know them are useless for audio because they do not have predictable performance at DC and/or 10GHz, cannot drive pure inductance or capacitance, etc., etc. Regardless of these claims, most amplifiers actually work just fine, and do not have to do any of the things that the claimants may imply. The vast majority of all the off-the-wall claims you will come across can safely be ignored.
It's also worth noting that making a design more complex (more parts) doesn't necessarily mean that it will have better performance. More active parts in the signal chain tend to add delays, and this can make it very difficult to keep the final circuit stable. No-one wants (or needs) an amplifier that has marginal stability, meaning that it may be on the verge of oscillation during normal operation. Connecting a speaker lead with above average capacitance may cause spurious (and intermittent) oscillations on parts of the waveform. This is always audible, but might not show up when the amp is on the test bench.
Power Opamp
Almost without exception, 'solid-state' power amplifiers can be considered to be a power opamp. The internal structure is typical of most opamps, but (usually) with lower overall complexity. Both power amps and opamps have inverting and non-inverting inputs, with the main (and most obvious) differences being the relative size, the supply voltages and output loads they can handle. They work the same way, feedback networks are between similar and identical, and they use the same set of stages internally.
The requirement for a power amplifier is to operate with supply voltages that can range from ±12V and ±100V, with the ability to drive up to 25A (sometimes more) into a load. A great deal of the design process is based on the output stage, where it's essential to ensure that the output transistors operate within their safe operating area (SOA) at all times. This not only influences the devices used, but also determines the heatsink requirements.
Unlike an IC opamp, a power amplifier needs careful attention to thermal management, and this still applies for IC power amps (which are also opamps, but perhaps with a few more features). Some of the most spectacular failures of commercial products have been based on the lack of proper thermal management. Note that this article does not cover heatsink selection/ design, but that is covered in the article on Heatsinks.
There are two main possibilities for an input stage for a power amplifier. The most common is the long tailed pair, so we shall look at this first. It's not uncommon to see two long-tailed-pairs, one using NPN and the other using PNP transistors. While this makes the circuit appear to be fully symmetrical, it isn't, because the NPN and PNP transistors will never be exact complements of each other.
Long Tailed Pair
It has been shown [ 1 ] that failing to balance the input Long Tailed Pair properly leads to a large increase in the distortion contributed by the stage. Some designers attempt to remedy the situation by including a resistor in the 'unused' collector circuit, but this is an aesthetic solution - i.e. it looks balanced, but serves no other useful purpose. (See Figure 1a) Note that the 'driver' transistor is simply there to allow us to make comparisons between the circuit topologies, and to provide current to voltage conversion. It is worth noting that even though this resistor serves no purpose electronically, it can make the PCB layout easier.
Use of the long-tailed (or differential) pair in an amplifier means that the amplifier will operate with what is generally called 'voltage feedback' (VFB). The feedback is introduced as a voltage, since the input impedance of both inputs is high (and approximately equal), and input current is (relatively speaking) negligible.
The feedback resistor and capacitor are selected to allow the circuit to operate at full open loop gain for the applied AC, but unity gain for DC to allow the circuit to stabilise correctly with a collector voltage at (or near) 0V. The transistors used in the simulations that follow are 'ideal', without internal capacitances etc, and have an hFE of 235 in all cases, measured with a base current of 10µA. The simulated circuits were operated at a voltage of ±12V. Different simulators will give different results, but the trends will be the same.
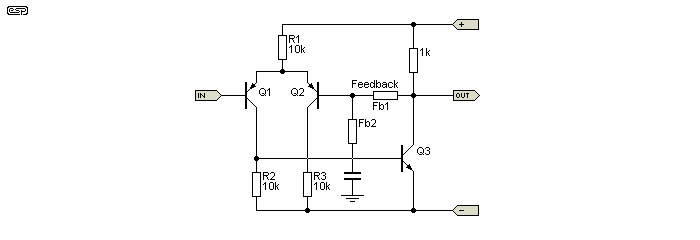
Figure 1a - Aesthetic Addition Of Resistor To Balance The Collector Load
As shown, and with a 12mA collector current for Q3, the load imbalance at the LTP collectors is 94µA for Q1, and 1mA for Q2. Simply by reducing the value of R1 it is possible to improve matters, but it is still not going to give the performance of which the circuit is capable. Again, as shown the gain of the LTP is a rather dismal 32 (as measured at the collector of Q2). The inclusion of R3 is purely cosmetic. It does provide a convenient means to measure the gain of the LTP, but otherwise serves no purpose.
Changing R1 for a current source does not help with gain, but provides a worthwhile improvement in power supply hum rejection, and in particular improves common mode rejection. A common mode signal is one that is applied in the same phase and amplitude to both inputs at once.
The overall gain of this configuration (measured at the collector of Q3) is 842, but by reducing R2 to 1.8k it can be raised to 1,850. This also improves collector current matching in the LTP, but the value will be device dependent, and is not reliable for production units.
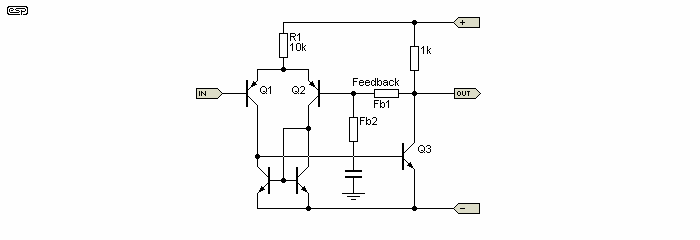
Figure 1b - A Current Mirror And Local Feedback Applied To The LTP
The circuit shown in Figure 1b has improved overall gain to 6,860, a fairly dramatic improvement on the earlier attempt. A further improvement in linearity is to be had by adding resistors (100 Ohm or thereabouts) into the emitter circuits of the current mirror transistors. This will swamp the base-emitter non-linearities, and provide greater tolerance to device gain variations. Overall gain is not affected.
Proper selection of the operating current will improve matters considerably, and also help to reduce distortion, especially if local negative feedback (as shown in Figure 1b) is applied. This has been discussed at length by various writers [ 1 ], and a bit of simple logic reveals that benefits are bound to accrue to the designer who takes this seriously.
Since the value of the transistor's internal emitter resistance (re) is determined by the current flow -
re = 26 / Ie (in mA)
At very low operating currents this value can be quite high. For example, at 0.5 mA, re will be about 52 ohms, increasing further as the current is reduced. Although this will introduce local feedback (and reduce the available gain), it is non-linear, resulting in distortion as the current varies during normal operation. Increasing the current, and using resistors (which are nice and linear) to bring the gain back to where it was before will reduce the distortion, since the resistor value - if properly chosen - will 'swamp' the variations in the internal re due to signal levels.
At small currents (where the current variation during operation is comparatively high), this internal resistance has a pronounced effect on the performance of the stage. Simple solutions to apparently complex problems abound.
Use of a current mirror as the load for the long-tailed pair (LTP) again improves linearity and gain, allowing either more local feedback elsewhere, or more global feedback. Either of these will improve the performance of an amplifier, provided precautions are taken to ensure stability - i.e. freedom from oscillation at any frequency or amplitude, regardless of applied load impedance.
There is another (not often used these days) version of an amplifier input stage. This is a single transistor, with the feedback applied to the emitter. It has been claimed by many that this is a grossly inferior circuit, but it does have some very nice characteristics. Technically, it uses current feedback, rather than the more common voltage feedback.
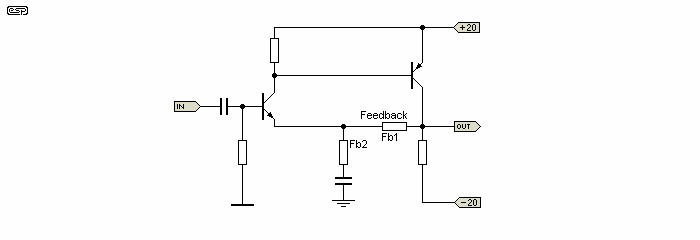
Figure 2a - Single Transistor Input Stage
So what is so nice about this? In a word, stability. An amplifier using this input stage requires little or no additional stabilisation (the 'Miller' cap, aka 'dominant pole') which is mandatory with amps having LTP input stages.
An amplifier using this input stage is referred to as a 'current feedback' (CFB) circuit, since the feedback 'node' (the emitter of the input transistor) is a very low impedance. The base circuit is the non-inverting input, and has a relatively high input impedance - but not generally as high as the differential pair. The +ve and -ve inputs are therefore asymmetrical. CFB amplifiers are used extensively in extremely fast linear ICs, and are capable of bandwidths in excess of 300MHz (that is not a misprint!).
This is the input stage used in the 10W Class-A amp (John Linsley-Hood's design, which is now part of TCCAS (The Class-A Audio Site), and also in the 'El-Cheapo' amp described in my Projects Pages. "Well if it is so good, why doesn't anybody use it?" I hear you ask (you must have said it pretty loudly, then, because Australia is a long way from everywhere  ).
).
There is one basic limitation with this circuit, and this was 'created' by the sudden requirement of all power amplifiers to be able to faithfully reproduce DC, lest they be disgraced by reviewers and spurned by buyers.
(I remain perplexed by this, since I know for a fact that I cannot hear DC, my speakers cannot reproduce it, I know of no musical instrument that creates it, and it would probably sound pretty boring if any of the above did apply. If you don't believe me, connect a 1.5V torch cell to your speaker, and let me know if I'm wrong. I seem to recall something about phase shift being bandied about at the time, but given the acoustics involved in recording in the studio and reproducing in a typical listening room - not to mention the 'interesting' phase shifts generated by loudspeaker enclosures as the speaker approaches resonance - I feel that the effects of a few degrees of low frequency phase shift generated in an amplifier are unlikely to be audible. This is of course assuming that human ears are capable of resolving absolute phase anyway - which they have been categorically proven to be unable to do.)
This input stage cannot be DC coupled (at least not without using a level shifting circuit), because of the voltage drop in the emitter circuit and between the emitter-base junction of the transistor. Since these cannot be balanced out as they are with an LTP input stage, the input must be capacitively coupled.
In addition, some form of biasing circuit is needed, and unfortunately this will either have to be made adjustable (which means a trimpot), or an opamp can be used to act as a DC 'servo', comparing the output DC voltage with the zero volt reference and adjusting the input voltage to maintain 0V DC at the output. The use of such techniques will not be examined here, but can provide DC offsets far lower than can be achieved using the amplifier circuit itself. There is no sonic degradation caused by the opamp (assuming for the sake of the discussion that decent opamps cause sonic degradation anyway), since it operates at DC only (it might have some small influence at 0.5Hz or so, but this is unlikely to be audible).
It has also been claimed that the single transistor has a lower gain than the LTP, but this is simply untrue. Open loop gain of the stage is - if anything - higher than that of a simple LTP for the same device current.
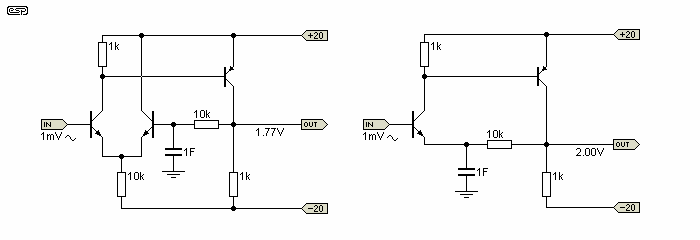
Figure 2b - Voltage Gain Comparison Of Input Stages
I simulated a very simple pair of circuits (shown in Figure 2b) to see the difference between the two. Collector current is approximately 1mA in each, and the output of the LTP shows a voltage gain of 1,770 from the combined circuit (the input stage cannot properly be measured by itself, since it operates as a current amp in both cases). In neither case did I worry about DC offset, since the effects are minimal for the purpose of simply looking at the gain - therefore offset is not shown. (Did you notice that the gains obtained in this simulation are completely different from those obtained earlier for the simple LTP circuit - I used a different voltage (the previous example used ±12V). This in no way invalidates anything, they are just different.)
By comparison, the open-loop gain of the single transistor stage is 2,000 - this (perhaps unexpectedly) is somewhat higher. Admittedly, the addition of a current mirror would improve the LTP even more dramatically, but do we really need that much more gain? A quick test indicates that we can get a gain of 3,570. This looks very impressive, but is only an increase of a little over 4.2dB compared to the single transistor. By the same logic, the single transistor only has a 1.06dB advantage over the simple LTP, however the difference may be moot ....
Because the single transistor stage requires no dominant pole Miller capacitor for stability, it will maintain the gain for a much wider frequency range, so in the long run might actually be far superior to the LTP. Further tests were obviously required, so I built them. Real life is never quite like the simulated version, so there was a bit less gain from each circuit than the simulator claimed. The LTP came in with an open loop gain of 1000, while the single transistor managed 1400. The test conditions were a little different from the simulation, in that ±15 volts was used, so the gain difference is about what would be expected, and is very close to the ±12V results obtained in the first set of simulations on the LTP.
Distortion was interesting, with the LTP producing 0.7% which was predominantly 3rd harmonic. The single transistor was slightly worse for the same output voltage with 0.9%, and this had a dominant 2nd harmonic. This is an open loop test, so it's really an examination of the 'worst-case' performance. If the gain is reduced with feedback, distortion falls dramatically. However, it doesn't necessarily fall in a direct relationship
As expected, the LTP was unstable without a Miller capacitor, and 56pF managed to tame it down. Quite unexpectedly, the single transistor also required a Miller cap, but only when running open-loop. When it was allowed to have some feedback the oscillation disappeared. The LTP could not be operated without the Miller capacitor at any gain, and as the gain approached unity, more capacitance was needed to prevent oscillation.
The next step was a test of each circuit providing a gain of about 27, since this is around the 'normal' figure for a 60W power amp. Here, the LTP is clearly superior, with a level of distortion I could not measure. The single transistor circuit had 0.04% distortion, and again this was predominantly 2nd harmonic. In this mode, no Miller capacitor was needed for the single transistor, and it showed a very wide frequency response, with a slight rise in gain at frequencies above 100kHz. This was also noticeable with a 10kHz square wave, which had overshoot, although this was reasonably similar for positive and negative half-cycles. The LTP was well behaved, and showed no overshoot (it had the 56pF Miller cap installed), but it started to run out of gain at about 80kHz, and there was evidence of slew-rate limiting. This effect was not apparent with the single transistor.
All in all, I thought this was a worthwhile experiment, and the use of a simple resistor for the collector load of the gain stage allowed the final circuit to have a manageable gain. Had a current source or similar been used as the load, I would not have been able to measure the gain accurately, since the input levels would have been too small. As it was, noise pickup proved to be a major problem, and it was difficult to get accurate results without using the signal averaging capability on the oscilloscope.
There are many designs that you'll see with what appear to be fully symmetrical input stages. It's implied that the symmetry improves performance, but it may be an illusion. While the schematic looks symmetrical, the fact is that the NPN and PNP devices (or N-Channel and P-Channel FETs) are not perfect mirror images of each other. There are usually easily measured differences between NPN and PNP devices from the same family, and datasheets will quickly disabuse you of the notion that they are the same.
There is some evidence to show that an apparently symmetrical input stage may be better than a more conventional asymmetrical stage, but there are countless very good amps that don't use the extra circuitry. In some bases, the symmetry is continued throughout the amplifier (the output stages are normally symmetrical anyway, but the Class-A gain stage usually is not). Again, it's easy to run simulations that may show that (apparent) symmetry improves things. However, it requires more parts, and if they don't make a significant (and audible) difference then they are basically wasted.
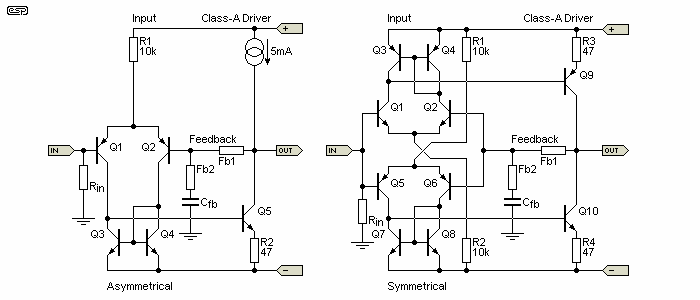
Figure 2C - Asymmetrical Vs. Symmetrical Input Stage Examples
The drawing above shows an example, but excluding any caps needed for stability. I included current mirrors, but only used a resistor to bias the two complementary long-tailed pairs. In reality, these would probably be replaced by current sources. While the circuit certainly looks 'nice and symmetrical', that doesn't mean that it really is, electrically speaking. In a simulation, one thing you'd really expect would be lower DC offset with the symmetrical arrangement, but in fact it simulated as being slightly worse. Depending on how the voltage amplifier stages are configured, the distortion can be less, greater, or about the same. My simulation shows lower distortion, but simulators use ideal parts, and real parts may not actually improve matters at all if the devices aren't carefully matched.
Note that I've only shown the input stage and Class-A amplifier (aka 'VAS' - voltage amplifier stage), and have not included output stage bias networks or the output stage itself. Feedback is normally taken from the output to the speakers, but as shown it works as intended for analysis. One distinct benefit of the symmetrical stage is that the output current is also symmetrical because it's push-pull, and isn't limited by the current available to the Class-A amplifier stage. This means greater drive is possible, but it also makes it easier to destroy the output stage if it doesn't have protection circuits. With no load, the current through the Class-A stages is roughly the same - 5mA.
None of this means that designs that are symmetrical are worse than asymmetrical designs, but nor does it mean that a symmetrical amp is necessarily 'better'. Many claims are made, but usually with little or no science to substantiate them. There are undoubtedly some very fine amplifiers that use symmetrical input and gain stages, just as there are many very fine amplifier that do not use symmetry as part of the design. It seems that to some people, what the circuit looks like is more important than how it performs. Sighted listening tests will invariably support this bias, and the myths become self-perpetuating.
A couple of things that help the symmetrical argument is lower noise (gain stages effectively in parallel, so gain is increased by 6dB, noise by 3dB). The gain is also higher, but this is not necessarily a good thing if it leads to instability, or requires much more complex networks to remain stable under all operating conditions. In amplifier design (and indeed virtually all electronics design), everything we do is ultimately a compromise, and it's the designer's job to get performance that meets or exceeds expectations, but not if it requires far greater complexity (unless it can't be avoided).
To obtain 'true' symmetry, use two amplifiers in BTL (bridge tied load) configuration. If the devices in each amplifier are matched, then the amplifier is completely symmetrical as far as the signal is concerned. Unfortunately, this comes with its own issues, not the least of which is that each amp 'sees' half the actual load impedance. That makes driving 4 ohm loads difficult, because the output current from each amp is double that which would be the case for a single amp driving the same impedance.
Very high current in BTL amps is always a problem, because the supply has to be able to provide it with minimal ripple, and transistors generally lose linearity at high currents. The entire amp becomes more complex (and expensive), but often with no genuine benefits. I've been asked about symmetrical designs many times, and my answer is the same - feel free to use a design, but don't expect it to measure (or sound) any better than a competently designed 'conventional' amplifier.
Based on the tests, there are pros and cons to all approaches (single transistor, long-tailed pair and symmetrical - and I'll bet that came as a surprise). The LTP in its simple form is a clear loser for gain, but use of a current mirror allows it to 'blow away' the single transistor, which cannot capitalise on this technique since there is nothing to mirror. Symmetrical inputs are considerably more complex, and you may (or may not) actually measure a difference between the simple LTP input and a symmetrical version.
Stability is very important to me, and I tend towards an amp which absolutely does not oscillate, even at the expense of a little more distortion. My own 60W reference amp is unconditionally stable with normal loads, and it uses an LTP for the input. Although I have experimented with symmetrical input stages, I have not published a design using this technique.
While there is no doubt at all that a symmetrical input stage can work very well, it does not automatically mean that the amp will sound any better. Adding the extra components makes the PCB more complex and the layout is critical. There's also a lot more to go wrong, especially with a compact input stage with many closely spaced transistors. Whether it's worth the effort depends on what you are trying to achieve, and you need to run tests to verify that what you think is 'better' is actually better. In many cases, a blind test may reveal that there's no audible difference, so the extra effort and parts serve no useful purpose.
A favourite pastime of many designers is to connect a small capacitor as shown in Figure 3 directly to the base of the input transistor. This is supposed to prevent detection (rectification) of radio frequency signals picked up by the input leads. Well, to a certain degree this is true, as the Resistor-Capacitor (RC) combination forms a low pass filter, which will reduce the amount of RF applied to the input. As shown this has a 3dB frequency of 159kHz (although this will be affected by the output impedance of the preceding stage).
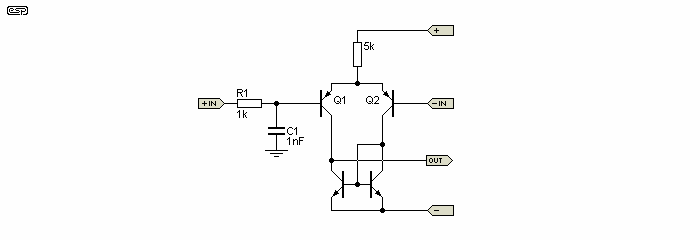
Figure 3 - The Traditional Method for Preventing RF Detection
This approach might work if PCB track lengths in that part of the circuit are very short, ensuring minimal inductance. This is not always the case, and some layouts may include more than enough track length to not only act as an inductor, but as an antenna as well. Then things can get really sneaky, such as when the levels of RF energy are so high that some amount manages to get through anyway. I once had a workshop/lab which was triangulated by three TV transmission towers - very nasty. RF interference was a fact of life there.
The traditional method not only did not work, but often made matters worse by ensuring that the transistor base was fed from a very low impedance (from an RF perspective) because of C1. A vast number of commercial amplifiers and other equipment which I worked on in that time picked up quite unacceptable amounts of TV frame buzz, caused by the detection of the 50Hz vertical synchronisation pulses in the TV signal. As the picture component of analogue TV is (or was - it's almost completely digital now) amplitude modulated RF, this was readily converted into audio - of the most objectionable kind.
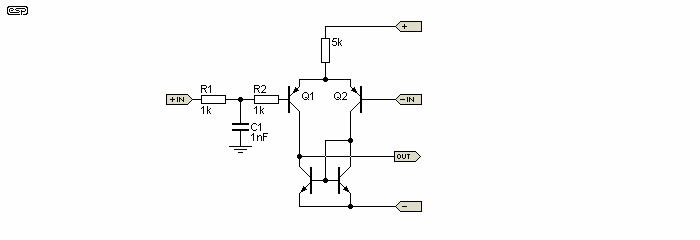
Figure 4 - Use of a Stopper Resistor to Prevent RF Detection
Figure 4 shows the remedy - but to be effective the R2 must be as close as possible to the base, or the performance is degraded. How does this work? Simple, the base-emitter junction of a transistor is a diode, and even when conducting it will retain non-linearities. These are often sufficient to enable the input stage to act as a crude AM detector, which will be quite effective with high-level TV or CB radio signals. Adding the external resistance again swamps the internal non-linearities, reducing the diode effect to negligible levels. This is not to say that it will entirely eliminate the problem where strong RF fields are present, but will at least reduce it to 'nuisance' rather than 'intolerable' levels.
UPDATE: I have been advised by a reader who works in a transmitting station that connecting the capacitor directly between base and emitter (in conjunction with the stopper resistor) is very effective. He too found that the traditional method was useless, but that when high strength fields are encountered, the simple stopper is not enough.
With opamps, the equivalent solution is to connect the stopper resistor in series with the +ve input, and the capacitor between the +ve and -ve inputs, with no connection to earth.
In all both cases it is essential to keep all leads and PCB tracks as short as possible, so they cannot act as an antenna for the RF. Needless to say, a shielded (and grounded) equipment case is mandatory in such conditions.
The Class-A amp stage is also commonly known as the Voltage Amplification Stage (VAS), but both terms are common, and are generally interchangeable. There are a number of traps here, not the least of which is that it is commonly assumed that the load (from the output stage) is infinite. Oh, sure, every designer knows that the Class-A stage must carry a current of at least 50% more than the output stage will draw, and this is easily calculated ...
IA = Peak_V / Op_R / Op_Gain × 1.5
where IA is the Class-A current, Peak_V is the maximum voltage across the load Op_R, and Op_Gain is the current gain of the output transistor combination.
For a typical 100W / 8 Ohm amplifier this will be somewhere between 5 and 10mA. Assuming an output transistor combination with a current gain of 1000 (50 for the driver, and 20 for the power transistor), with an 8 Ohm load, the impedance presented to the Class-A stage will be about 2k Ohms, which is a little shy of infinity.
Added to this is the fact that the impedance reflected back is non-linear, since the driver and output transistors change their gain with current - as do all real-life semiconductors. There are some devices available today which are far better than the average, but they are still not perfect in this respect.
The voltage gain is typically about 0.95 to 0.97 with the compound pair configuration. It must be noted that this figure will only be true for mid-range currents, and will be reduced at lower and higher values. Figure 5 shows the basic stage type - the same basic amplifier we used before, with the addition of a current source as the collector load. Also common is the bootstrapped circuit (not shown here, but evident on many ESP designs).
There is not a lot of difference between current source and bootstrap circuits, but the current source gives slightly higher gain. With either type, there are some fairly simple additions which will improve linearity quite dramatically. Figure 5 shows the typical arrangement, including the 100pF dominant pole stabilisation capacitor connected between the Class-A transistor's collector and base.
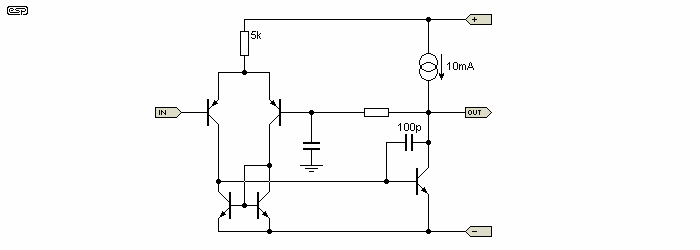
Figure 5 - Typical Class-A Driver Configuration
It is important to try to make the Class-A stage capable of high gain, even when loaded by the output stage. There have been many different methods used to achieve this, but none is completely successful. The output stage is not a simple impedance, and it varies as the load impedance changes. Bipolar transistors reflect the load impedance back to the base, adjusted according to the device's gain. A potential problem is that some designers seem completely oblivious to this problem area, or create such amazingly complex 'solutions' as to make stabilisation (against oscillation) very difficult.
This is one area where MOSFETs may be found superior to BJTs. The gate capacitance is not affected by the load impedance, and nothing is reflected back to the Class-A driver. This will typically allow it to have higher gain - especially when low load impedances are involved. The Class-A driver needs only to be able to charge and discharge the gate capacitance of the MOSFETs, and this is not influenced by the output current or load.
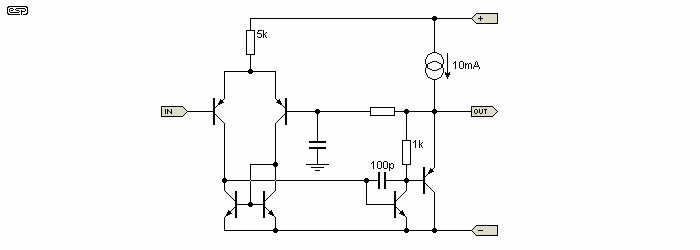
Figure 6 - Improving Open Loop Output impedance of Class-A Driver
The above is simple and very effective. This straightforward addition of an emitter follower to the Class-A driver (with the 1k 'bootstrap' resistor) has increased the combined LTP and Class-A driver gain to 1,800,000 (yes, 1.8 million!) or 125dB (open loop and without the dominant pole capacitor connected). Open loop output impedance is about 10k, again without the cap. Once the latter is in circuit, gain is reduced to a slightly more sensible 37,000 at 1kHz with the 100pF value shown. Output impedance at 1kHz is now (comparatively) very low, at about 150 Ohms.
Note that in the above, I have used a 5k resistor instead of the more usual current source to bias the long-tailed pair. This is for clarity of the drawing, and not a suggestion that the current source should be forsaken in this position.
A special note for the unwary - If one is to use a single current control transistor for both the LTP and Class-A driver, do not use the Class-A (aka VAS - voltage amplifier stage) current as the reference, but rather the LTP. If not, the varying current in the Class-A circuit will cause modulation of the LTP emitter current, with results that are sure to be as unwelcome as they are unpredictable [ 4 ]. Where the current source reference is based on the VAS (Class-A driver), it's advisable to decouple the voltage reference for the LTP source to minimise interactions.
I have often seen amplifier designs where the circuit is of such complexity that one must wonder how they ever managed to stop them from becoming high power radio frequency oscillators. The maze of low value capacitors sometimes used - some with series resistance - some without, truly makes one wonder what the open loop frequency and phase response must look like. Couple this with the fact that many of these amps do not have wonderful specifications anyway, and one is forced to ponder what the designer was actually trying to accomplish (being 'different' is not a valid reason to publish or promote a circuit in my view, unless it offers some benefit otherwise unattainable).
Having carried out quite a few experiments, I am not convinced that vast amounts of gain from the input stage and Class-A amplifier stage are necessary or desirable. As long as the circuit is linear (i.e. has low distortion levels before the addition of feedback), the final result is likely to be satisfactory. I have seen many circuits with far more open loop gain than my reference amp (Project 3A), that in theory should be vastly superior - yet they apparently are not.
There are essentially two ways to create a constant current feed to the Class-A driver stage. The active current source is one method, and this is very common. It does introduce additional active devices, but it is possible to make a current source that has an impedance so close to infinity that it will be almost impossible to measure it without affecting the result just by attaching measurement equipment. For more detailed information on current sources, see the article Current Sources Sinks and Mirrors. Figure 6A shows an active current source for reference.
A simpler way is to use the bootstrap circuit, where a capacitor is used from the output to maintain a relatively constant voltage across a resistor. If the voltage across a resistor is constant, then it follows that the current flowing through it must also be constant. Figure 6a shows the circuit of a bootstrap constant current source. Unlike a true current source, the current through the bootstrap circuit will change with the supply voltage. This is a gradual change, and is outside the audio spectrum - or at least it should be if the circuit is designed correctly.
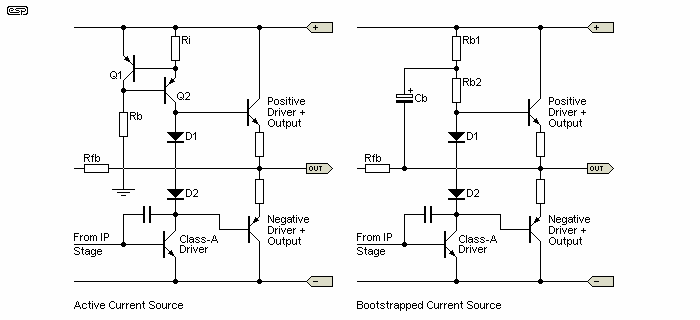
Figure 6A - Active And Bootstrapped Current Source
The bootstrap circuit works as follows. Under quiescent conditions, the output is at zero volts, and the positive supply is divided by Rb1 and Rb2. The base of the upper transistor will be at about +0.7V - just sufficient to bias the transistor. As the output swings positive or negative, the voltage swing is coupled via Cb, so the voltage across Rb2 remains constant. The current through Rb2 is therefore constant, since it maintains an essentially constant voltage across it. Note that this applies only for AC voltages, as the capacitor cannot retain an indefinite charge if there is a DC variation.
The overall difference is not great in a complete design. Although the current source is theoretically better, a bootstrap circuit is simpler and cheaper, and introduces no additional active devices. The capacitor needs to be large enough to ensure that the AC across it remains small (less than a few hundred millivolts) at the lowest frequency of interest. Assuming Rb1 and Rb2 are equal, the cap's voltage rating needs to be a minimum of ½ the positive supply voltage, but preferably greater.
The output stage is - usually - a current amplifier only. Voltage gain is provided by the previous stage (the VAS), and the current is amplified by the output devices. The combination of voltage and current amplification means that power is amplified. The input power may be around 50μW (1V into 22k), and the output power (say) 100W. This represents a power gain of 2 million (63dB) for the complete amplifier. These are examples only - there will be differences, but it's not something that anyone generally considers. It does become an important factor for RF (radio frequency) amplifiers, but they are not covered here.
The current amplifier is most commonly a pair of emitter-followers, generally either Darlington or Sziklai pairs, offering a current gain of 1,000 or more. More complex arrangements are sometimes used (e.g. triple 'Darlington') to get more current gain, reducing the loading on the VAS. With MOSFETs, the arrangement is a complementary source-follower. These have the advantage of almost infinite current gain because there's very little load imposed on the VAS, but MOSFETs are slightly less linear than BJTs as followers, and show a small loss of voltage gain. The output voltage is usually about 0.97 compared to the input voltage, compared to 0.99 for Darlington/ Sziklai connected BJTs. MOSFETs also have a somewhat higher 'on' voltage (Rds-on), and that can reduce the theoretical peak output power available. However, the loss is rarely more than 1dB, and is not usually a major limitation.
There are a small number of designs that use an output stage with gain. While this is theoretically a good idea, in practice you end up with a stage that has poor thermal stability and higher open-loop distortion than any of the other arrangements. This is shown below, along with analysis of its shortcomings. However, it remains a viable option in some cases, so it should not be discounted out of hand. Any arrangement that meets the requirements of the designer can be made to work well, but some are harder than others.
There are countless amplifiers which still use the Darlington type configuration, even though this was shown by many [ 2 ] to be inferior to the Sziklai/ complementary pair. Both configurations (in basic form, since there are many variations) are shown in Figure 7. There are two main areas where the Darlington configuration is inferior, and we shall look at each. In the following, bias networks and Class-A driver(s) are not included, only the output and driver transistors ...
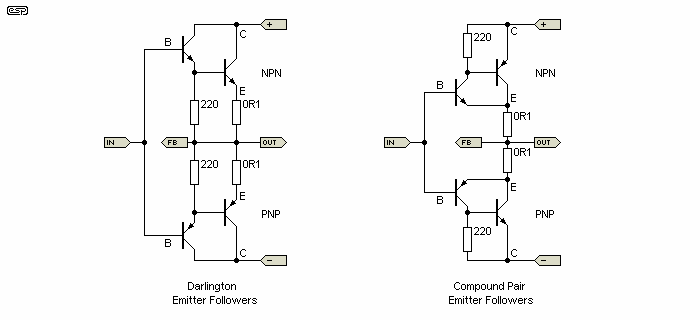
Figure 7 - The Basic Configurations Of Output Stages In Common Use
Of the two shown, it will be apparent that I have not included MOSFET output stages - this is because MOSFETs require no driver transistor as such - they are normally driven directly from the Class-A amplifier (or a modified version - often an additional long-tailed pair. As can be seen, the component count is the same for those shown, but instead of using two same polarity (both PNP or both NPN), the compound pair (also called a Sziklai pair) uses one device of each polarity. The final compound device assumes the characteristics of the driver in terms of polarity, and the Emitter, Base and Collector connections for each are shown. The 220 ohm resistor (or other value determined by the design) is added to prevent output transistor collector to base leakage current from allowing the device to turn itself on, and also speeds up the turn-off time. Omission of this resistor is not a common mistake to make, but it has been done. In some cases, you'll see a comparatively high value used. The results are degraded distortion figures, especially at high frequency, and poor thermal stability.
The value must be selected with reasonable care, if it is too low, the output transistor will not turn on under quiescent (no signal) conditions, the driver transistor(s) will be subject to excessive dissipation, and crossover distortion will result. If too high, turn-off performance of output devices will be impaired and thermal stability will not be as good. The final value depends (to some extent) on the current in the Class-A driver stage and the gain of the driver transistor, but the final arbiter of quiescent is the Vbe multiplier stage. These comments apply equally to the Darlington and compound pairs.
Values of between 100 Ohms up to a maximum of perhaps 1k should be fine for most amplifiers, with lower values used as power increases. High power creates higher currents throughout the output stage and makes the transistors harder to turn off again, especially at high frequencies. This can lead to a phenomenon called 'cross-conduction', which occurs because the transistors cannot switch off quickly enough, so there is a period where both power transistors are conducting simultaneously. It won't happen at normal audio frequencies, although you may get slightly higher than normal current drawn from the power supply even at 20kHz.
If an amp is driven to any reasonable power at higher frequencies, it can spontaneously self-destruct if there is sufficient cross conduction happening. The easiest way to reduce it is to use smaller resistors between base and emitter of the power transistors, but be aware that this will increase the demands on the drivers. For example, with 220 ohm resistors as shown above, the resistors will only pass around 3-5mA, but if they are reduced to (say) 47 ohms, that increases to perhaps 16mA or more. The drivers have to supply this current, even at idle, and their quiescent power dissipation increases from 120mW to over 550mW with ±35V supplies. A heatsink for the drivers becomes a necessity.
Normally, there should be little or no need to use resistors less than ~100 ohms. If you want to get full power at 100kHz or more (why? it serves no purpose for an audio amplifier), then you'll need to make these resistors even lower in value and ensure proper heatsinks for the drivers. You will also need to increase the power rating for the Zobel network resistor, or it will overheat at high frequencies.
It can be seen that in the Darlington configuration, there are two emitter-base junctions for each output device. Since each has its own thermal characteristic (a fall of about 2mV per degree C), the combination can be difficult to make thermally stable. In addition, the gain of transistors often increases as they get hotter, thus compounding the problem. The bias 'servo', typically a transistor Vbe multiplier, must be mounted on the heatsink to ensure good thermal equilibrium with the output devices, and in some cases can still barely manage to maintain thermal stability.
If stability is not maintained, the amplifier may be subject to thermal runaway, where after a certain output device temperature is reached, the continued fall of Vbe causes even more quiescent current to flow, causing the temperature to rise further, and so on. A point is reached where the power dissipated is so high that the output transistors fail - often with catastrophic results to the remainder of the circuit and/or the attached loudspeakers.
The Sziklai/ compound pair has only one controlling Vbe, and is thus far easier to stabilise. Since the single Vbe is that of the driver (which should not be mounted on the main heatsink, and in some will have no heatsink at all), the requirements for the Vbe multiplier are less stringent, mounting is far simpler and thermal stability is generally very good to excellent.
I have used the compound pair since the early 1970s, and when I saw it for the first time, it made too much sense in all respects to ignore. Thermal stability in a fairly basic 100W/4 Ohm amplifier of my design (of which many hundreds were built - it was the predecessor of the P3A design in the projects section) was assured with a simple 2-diode string - no adjustment was ever needed. (However, there were a couple of other tricks used at the time to guarantee stable operation.)
It would seem (at first glance at least) that there is nothing to this piece of circuitry. It is a very basic Vbe multiplier circuit, and seemingly, nothing can go wrong. This is almost true, except for the following points.
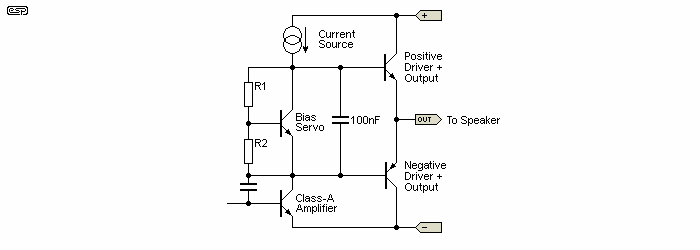
Figure 9 - The Basic Bias Servo Circuit
The design of many amps (especially those using a Darlington output stage) requires that the bias servo be made adjustable, to account for the differing characteristics of the transistors. If resistor R1 (in Fig 9) is instead a trimpot (i.e. variable resistor), what happens when (if) the wiper decides (through age, contamination or rough handling) to go open-circuit?
The answer is simple - the voltage across the bias servo is now the full supply voltage (less a transistor drop or two), causing both the positive and negative output devices to turn on as hard as they possibly can. The result of this is the instantaneous destruction of the output devices - this will happen so fast that fuses cannot possibly prevent it, and even the inclusion of sophisticated Load-Line output protection circuitry is unlikely to be able to save the day.
The answer of course is so simple that it should be immediately obvious to all, but sadly this is not always the case. By making R2 the variable component, should it happen to become open-circuited the bias servo simply removes the bias. This will introduce crossover distortion, but the devices are saved. To prevent the possibility of reducing the pot value to 0 ohms (which will have the same effect as described above!), there is often a series resistor, whose value is selected to allow adequate adjustment while retaining a respectable safety margin. It's not essential, provided that the setup instructions are followed carefully.
An additional precaution must be taken here, in that if the resistor values are too low, the offset voltage seen by the output transistors is simply the voltage drop across the resistors, with the transistor having little or no control over the result. This is easily avoided by ensuring that the resistor current is 1/10 (or thereabouts) of the total Class-A bias current.
It is also possible to make the resistance too large, and the bias servo will be less stable with varying current. This may also cause the bias servo to have too much gain, which can cause the amplifier's quiescent current to fall as it gets hotter. While this is a good thing from the reliability point of view, if it causes crossover distortion to appear when the amp is hot, the audible effect will obviously be disappointing. It will generally be necessary to experiment with the values to ensure that stability is maintained - there is no way to calculate this that comes to mind, although I am sure it is possible. The base-emitter voltage falls at 2mV /°C, but the variation in gain with temperature is not as readily calculated.
As a secondary safeguard, using a suitable diode string in parallel with the servo may be useful. These should be chosen to prevent destructive current, but some method of over temperature protection will be needed. This can be a fan blowing onto the heatsink, or a thermal cutout to switch off the power if the amp gets too hot.
Note that if the output stage uses the Darlington arrangement, the bias servo transistor must be located on the main heatsink. If you use a compound (Sziklai) pair, it is imperative that the bias servo senses the driver transistor(s) (which should not be on the main heatsink). Failure to locate the bias servo properly is inviting output stage failure due to thermal runaway.
Numerous articles have been written on the superior linearity of the compound (Sziklai) stage (Otala [ 3 ], Self, Linsley Hood among others) and I cannot help but be astonished when I see a new design in a magazine, still using the Darlington arrangement. The use of the compound pair requires no more components - the same components are simply arranged in a different manner. It was with great gusto that an Australian electronics magazine proudly announced (in 1998) that "this is the first time we have used this arrangement in a published design" (or words to that effect). I don't know the reason(s) they may have had for not using the complementary pair in every design they published (this magazine is a lot younger than I). Words fail me. The magazine in question is not the only one, and the Web abounds with designs old and new - all using the Darlington emitter-follower.
This is not to say that the Darlington stage shouldn't be used - there are many fine amplifiers that use it, and with a bit of extra effort to get the bias servo right, such amps will give many years of reliable service. It is particularly suited to very high power amps, because of its simplicity - especially with multiple paralleled output devices. Parallel operation is more irksome with the Sziklai configuration. An example of paralleled Sziklai pairs is seen in Project 27. Having to use additional emitter resistors for each output transistor (in series with its physical emitter) is a nuisance, but the arrangement works very well indeed.
| Darlington | ||
| Driver | O/P Transistor | Total Gain |
| 50 | 25 | 1310 |
| Compound (Sziklai) | ||
| Driver | O/P Transistor | Total Gain |
| 50 | 25 | 1290 |
The lower gain of the compound pair indicates that there is internal local negative feedback inherent in the configuration, and all tests that have been performed indicate that this is indeed true. Although the gain difference is not great, much of the improved linearity can be assumed to result from the fact that only one emitter-base junction is directly involved in the signal path rather than two, so only one set of direct non-linearities is brought into the equation. The second (output) device effectively acts as a buffer for the driver.
Having said that, there are some very well respected amplifiers using Darlington emitter-follower output stages. There are no hard and fast rules that can be applied to make the perfect amplifier (especially since it does not yet exist), and with careful design it is quite possible to make a very fine amplifier using almost any topology.
One thing that can (and does) cause problems is the output stage gain. If it's biased to a lower than optimum current, the gain falls dramatically. If the output stage's current gain falls too far, the entire amplifier effectively has no gain, so negative feedback can do nothing to reduce crossover distortion. This is why an amplifier should be as linear as possible before the application of feedback, but claims that feedback "ruins the sound" are divorced from reality. While it's possible to design an amplifier with no feedback, there's really very little point. It won't perform as well as a more conventional design, regardless of 'reviews' that may extol it's alleged virtues.
It is a simple fact of life that an emitter follower (whether Darlington or compound) is perfectly happy to become an oscillator - generally at very high frequencies. This is especially true when the output lead looks like a tuned circuit. A length of speaker cable, while quite innocuous at audio frequencies, is a transmission line at some frequency determined by its length, conductor diameter and conductor spacing. A copy of the ARRL handbook (from any year) will provide all the formulae needed to calculate this, if you really want to go that far.
All power amplifiers (well, nearly all) use emitter follower type output stages, and when a speaker lead and speaker (or even a non-inductive dummy load) are connected, oscillation often results. This is nearly always when the amp is driven, and is more likely when current is being drawn from the circuit. It is a little sad that the compound pair is actually more prone to this errant behaviour than a Darlington, possibly because the driver is the controlling element (and its emitter is connected to the load), and has a higher bandwidth.
Some of the 'super' cables - much beloved by audiophiles - are often worse in this respect for their ability to act as RF transmission lines than ordinary Figure-8, zip cord or 3-core mains flex, and are therefore more likely to cause this problem.
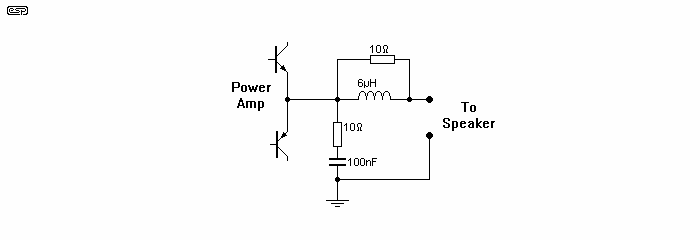
Figure 10 - The Standard Output Arrangement For Power Amp Stability
The conventional Zobel network (consisting of the 10 Ohm resistor and 100nF capacitor) generally swamps the external transmission line effect of the speaker cables and loudspeaker internal wiring, and provides stability under most normal operating conditions.
In a great many amplifiers, the amp may oscillate with no load or speaker cables attached, and a Zobel network as shown stops this, too. The reasons are a little difficult to see at first, but can be traced to small amounts of stray inductance and capacitance around the output stage in particular. At very high frequencies, these strays can easily form a tuned circuit, causing phase shift between the amp's output and inverting input. At these high frequencies, few amplifiers have a great deal of phase margin (the difference between the amplifier's phase shift and 180°). Any stray inductance and/or capacitance may only need to create a few additional degrees of phase shift to cause oscillation. Because there is very little feedback at such high frequencies, the overall impedance can be much higher than expected.
At these frequencies, the Zobel capacitor is essentially a short circuit, so there is now a 10 ohm resistor in parallel with a high impedance tuned circuit. The 10 ohm resistor ruins the Q of the tuned circuit(s), and applies heavy damping, thus negating the phase shift to a large degree and restoring stability. Personally, I don't recommend that this network be omitted from any amplifier, even if it appears to be stable without it.
With capacitive loading (as may be the case when a loudspeaker and passive crossover are connected), the Zobel network has very little additional effect - may have no effect whatsoever. The only sure way to prevent oscillation or severe ringing with highly capacitive cables is to include an inductor in the output of the amplifier. This should be bypassed with a suitable resistor to reduce the Q of the inductor, and the typical arrangement is shown in Fig 10. For readers wishing to explore this in greater depth, read 'The Audio Power Interface' [ 2 ]. In many cases it might be better to use a far lower resistance than the 10 Ohms normally specified - I am thinking around 1 Ohm or so. Some National Semiconductor power opamps specify 2.7 ohms as the optimum. Ideally, cables with low inductance and high capacitance should always have an additional 100nF/10 ohm Zobel network at the loudspeaker end. When this is done, the cable no longer appears as a capacitor at high frequencies. Regrettably, few (if any) loudspeaker manufacturers see fit to include this at the input terminals.
Another alternative is to include a resistor in series with the output of the amplifier, but this will naturally have the dual effect of reducing power output and reducing damping factor. At resistor values sufficient to prevent oscillation, the above losses become excessive - and all wasted power must be converted into heat in the resistor.
The choice of inductor size is not difficult - for an 8 Ohm load it will be typically a maximum of 20µH, any larger than this will cause unacceptable attenuation of high frequencies. A 6µH inductor as shown in Figure 10 will introduce a low frequency loss (assuming 0.03 Ohm resistance) of 0.03dB and will be about 0.2dB down at 20kHz. These losses are insignificant, and will not be audible. In contrast, ringing (or in extreme cases, oscillation) of the output devices will be audible (even at very low levels) as increased distortion, and in extreme cases may destroy the transistors.
It is not realised by everyone, but a single unity gain transistor stage can oscillate. Opamps and power amps commonly use emitter followers for their outputs, and failure to isolate the transistor stage from cable effects can (and regularly does) cause the stage to oscillate. All opamps that connect to the outside world (via connectors on the front or rear panel for example) must use a series resistor. Values from 47 ohm up to 220 ohms are usually enough. I use 100 ohms as a matter of course, but lower (or higher) values may be needed, depending on what you are trying to achieve.
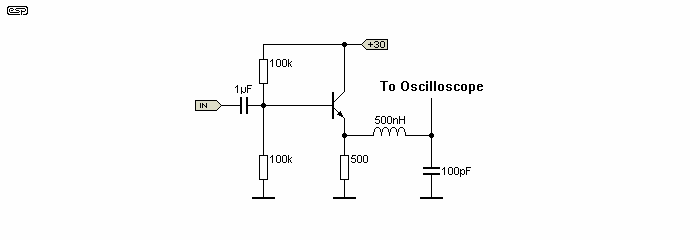
Figure 11 - Lumped Component Transmission Line Causes Emitter Follower To Oscillate
In simulations and on the lab bench, I have been able to make a single transistor emitter follower circuit oscillate quite happily, with a real transmission line (such as a length of co-axial cable), or a lumped component equivalent of a transmission line, consisting of a 500µH inductor and 100pF as a series tuned circuit. This is shown in Figure 11.
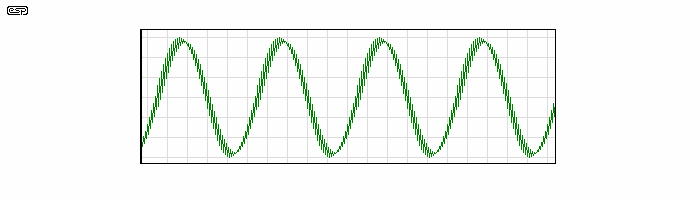
Figure 12 - Simulator Oscilloscope Display Of Oscillation In Emitter Follower
This effect is made worse as the source impedance is lowered, but even a base stopper resistor will not prevent oscillation - only the swamping effect of the transmission line by a Zobel network or a series resistance succeeds. In case you were wondering why the oscilloscope take-off point is at the junction of the L and C components, this allows series resonance to amplify the HF component, making it more readily seen.
For power amplifiers, this problem is solved by using a Zobel network, optionally with a series inductor. For low-level stages, it is more sensible to use a resistor in series with the output. The resistor is normally between 22 and 100 ohms, and this will be seen in all ESP designs where an opamp connects to the outside world (or even an internal cable). A resistor can be used with power amps too, but at the expense of power loss, heat, and loss of damping factor. For a power amp, the output inductor can be replaced by a 1 ohm resistor (sometimes less), but this is extremely rare.
In my own amp (P3A being the latest incarnation), I did not use an output inductor, but instead made the dominant pole (the capacitance from the collector to base of the Class-A driver) a little larger than you mat see in other designs. This keeps the amp stable under all operating conditions, but at the expense of slew rate (and consequent slew rate limited power at high frequencies). This was initially largely an economic decision, since a couple of ceramic capacitors are much cheaper than an inductor, and the amp was used in large numbers at the time largely for musical instrument amplification, so an extended high frequency response was actually undesirable. Full power bandwidth - the ability of an amp to supply full power over its entire operating frequency range - is a sure way to destroy hearing, HF horn drivers (etc) in a live music situation, so the compromise was not a limitation. P3A does allow the value to be changed, provided you have an oscilloscope and can check for (sometimes parasitic) oscillation. However ...
There is another reason that a series output inductor may be helpful. It has been suggested (but by whom I cannot remember) that radio frequencies picked up by the speaker leads may be injected back into the input stage via the negative feedback path. When one looks at a typical circuit, this seems plausible, but I have not tested the theory too deeply.
The basics behind it are not too difficult to work out. Since it is known that there must be a dominant pole in the amplifier's open-loop frequency response (the capacitor shown in all figures including a Class-A amp stage) if it is to remain stable when feedback is applied, it follows that as internal gain decreases with increasing frequency then the output impedance must rise (due to less global feedback). Indeed this is the case, and by the time the frequency is into the MHz regions, there will be negligible loading of any such frequencies by the output stage.
If appropriate precautions are not taken (as in Figure 4) for the negative feedback return path, then it is entirely likely that RF detection could occur. In my own bi-amped system (which uses the predecessor of the P3A amplifier described above, still without an output inductor), I recently had problems with detection of a local AM radio station. Fitting of RF 'EMI' suppression chokes (basically, loop the speaker cable through a ferrite ring 3 or 4 times) completely eliminated the problem, so I must conclude that it is indeed possible or even probable.
If an amplifier is ever likely to be connected to 'exotic' (expensive 'audiophile') cables then it is essential that an output inductor is used. As noted above, the inductance has to be limited to prevent high frequency rolloff, and for load impedances down to 4 ohms, the inductance should not exceed about 10µH. In most cases, as many turns as will fit onto a 10 ohm 1W resistor will be sufficient, and the wire used must be thick enough to carry the full speaker current.
The maximum output current of a power amplifier is often thought to be something that affects the output transistors only, and that adding more transistors will automatically provide more current to drive lower impedances. This is only partially true, because bipolar transistors need base current, and this must come from the driver stage.
It is common to bias the Class-A driver stage so that it can provide between 1.5 to 5 times the expected base current needed by the output transistors and their drivers. As the current in this stage is lowered, there is likely to be a substantial increase in the distortion, since the current will change by a larger percentage. If the Class-A driver current is too high, there will be too much heat to get rid of, and it is possible to exceed the transistor's maximum ratings. I normally work to a figure of about double the expected output device base current, but in some cases it will be more or less than this. We also have to design around the lowest expected current gain for all transistors used.
As an example, let's look at a typical power amplifier output stage. Assuming a power supply of ±35V, the maximum output current will be 35 / 8 = 4.375 Amps (an 8 ohm load is assumed). Since we know that there will be some losses in the driver / power transistor combination, we can safely assume a maximum (peak) current of 4A. A suitable power transistor may be specified for a minimum gain (hFE) of 25, with a collector current of 4A. The driver transistors will generally have a higher gain - perhaps 50 at a collector current of 250mA. The product of the two current gains is accurate enough for what we need, and this gives a combined hFE of 1,000. The peak base current will therefore be 4mA.
If we choose to use a Class-A driver current of double the expected output device base current, this means that the driver will operate at about 8mA. This could be achieved with a current source, or a bootstrapped circuit using a pair of 2.2k resistors in series. At the maximum voltage swing (close to ±35V), the driver current will be increased to 12mA or decreased to 4mA, depending on the polarity. The current source or bootstrap circuit will maintain a constant current, but the driver has to deal with a current that varies by ±4mA as the current into the load changes.
If the load impedance is dropped to 4 ohms, the current source will still only be able to provide 8mA, so output current will be limited to 8A - the driver at this point in the cycle has zero current. At the opposite extreme, the driver will have to cope with 16mA when it is turned on fully. At lower impedances, the driver will be able to supply more current, but the current source will steadfastly refuse to provide more than the 8mA it was designed for, so the peak output current will be limited to 8A in one direction (when the current source provides the drive signal and the Class-A driver is turned off), or some other (possibly destructive) maximum current in the opposite polarity.
But hang on! A Class-A driver is called a Class-A driver because it never turns off - we now have a Class-AB driver, which is not the desired objective and doesn't even work for a single-ended amplifier stage! The power amplifier will clip asymmetrically, and is no longer operating in the linear range - it is distorting.
Adding more power transistors will provide a very limited benefit, since the maximum base current is still limited by the current source supplying the Class-A driver. In order to obtain maximum power at lower impedances requires that either the gain of the output stage is increased, or the Class-A driver current must be increased. Increasing the gain of the output stage devices is not trivial - you must either use a different topology or higher gain power and driver transistors.
The design phase of an amplifier follows similar guidelines, regardless of topology. From Amplifier Basics ...
Power Output vs. ImpedanceThe power output is determined by the load impedance and the available voltage and current of the amplifier. An amplifier that is capable of a maximum of 2A output current will be unable to provide more just because you want it to. Such an amp will be limited to 16W 'RMS' into 8 ohms, regardless of the supply voltage. Likewise, an amp with a supply voltage of ±16V will be unable to provide more than 16W into 8 ohms, regardless of the available current. Having more current available will allow the amp to provide (for example) 32W into 4 ohms (4A peak current) or 64W into 2 ohms (8A peak current), but will give no more power into 8 ohms than the supply voltage will allow.Driver CurrentEspecially in the case of bipolar transistors, the driver stage must be able to supply enough current to the output transistors - with MOSFETs, the driver must be able to charge and discharge the gate-source capacitance quickly enough to allow you to get the needed power at the highest frequencies of interest.Class-A Driver Stage
For the sake of simplicity, if bipolar output transistors have a gain of 20 at the maximum current into the load, the drivers must be able to supply enough base current to allow this. If the maximum current is 4A, then the drivers must be able to supply at least 200mA of base current to the output devices.The stages that come before the drivers must be able to supply sufficient current for the load imposed. The Class-A driver of a bipolar or MOSFET amp must be able to supply enough current to satisfy the base current needs of bipolar drivers, or the gate capacitance of MOSFETs.Input Stages
Again, using the bipolar example from above, the maximum base current for the output transistors was 200mA. If the drivers have a minimum specified gain of 50, then their base current will be ...
200 / 50 = 4mA.Since the Class-A driver must operate in Class-A (what a surprise), it will need to operate with a current of 1.5 to 5 times the expected maximum driver transistor base current, to ensure that it never turns off. The same applies with a MOSFET amp that will expect (for example) a maximum gate capacitance charge (or discharge) current of 4mA at the highest amplitudes and frequencies. For the sake of the exercise, we shall assume a Class-A driver (VAS) current of double the base current needs of the drivers ... 8mA.The input stages of all transistor amps must be able to supply the base current of the Class-A driver. This time, a margin of between 2 and 5 times the expected maximum base current is needed. If the Class-A driver operates with a quiescent current of 8mA, the maximum current will be 12mA (quiescent + driver base current). Assuming a gain of 50 (again), this means that the input stage has to be able to supply 12 / 50 = 240µA, so it must operate at a minimum current of 240µA × 2 = 480µA to preserve linearity.Input CurrentThe input current of the first stage determines the input impedance of the amplifier. Using the above figures, with a collector current of 480µA, the base current will be 4.8µA for input devices with a gain of 100. If maximum power is developed with an input voltage of 1V, then the impedance is 208k ( R = V / I ).
Since the stage must be biased, we apply the same rules as before - a margin of between 2 and 5, so the maximum value of the bias resistors should be 208 / 2 = 104k. A lower value is preferred, and I suggest that a factor of 5 is more appropriate, giving 208 / 5 = 42k (47k can be used without a problem).
These are only guidelines (of course), and there are many cases where currents are greater (or smaller) than suggested. The end result is in the performance of the amp, and the textbook approach is not always going to give the result you are after. Remember that higher value resistors mean greater thermal noise, although this is rarely a problem with power amps.
Be careful if you decide to use a lower than normal feedback resistor, as it may run quite hot. A 100W (8 ohm) amp will have about 28V across the feedback resistance, so a 22k resistor will dissipate 35mW. Reduce that to 1k (which would be silly for a variety of reasons), and dissipation is nearly 800mW. Of course, increasing the amplitude increases dissipation by the square of the voltage, so even a 22k resistor will dissipate over 220mW in a 600W amplifier.
Reality is different of course - we generally don't listen to full power sinewaves, and normal music keeps the feedback resistor cool enough not to cause problems in the majority of designs. Resistors that are run close to their maximum power (or voltage) ratings have a much shorter life than those that run cool and/or well within voltage ratings. And yes, resistors do have voltage ratings that are independent of their power rating.
When specified, transformer regulation is based upon a resistive load over the full cycle, but when used in a capacitor input filter (99.9% of all amplifier power supplies), the quoted and measured figures will never match.
Since the applied AC from the transformer secondary spends so much of its time at a voltage lower than that of the capacitor, there is no diode conduction. During the brief periods when the diode conducts, the transformer has to replace all energy drained from the capacitor in the intervening period between diode conductions, as well as provide instantaneous output current.
Consider a power supply as shown in Figure 13. This is a completely conventional full-wave capacitor input filter (it is shown as single polarity for convenience). The circuit is assumed to have a total effective series resistance of 1 Ohm - this is made up by the transformer winding resistances (primary and secondary). The capacitor C1 has a value of 4,700µF. The transformer has a secondary voltage of 28V. Diodes will lose around 760mV at full power.
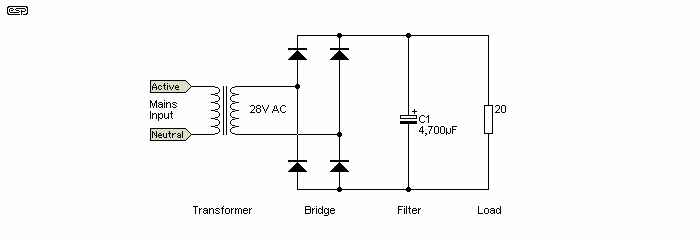
Figure 13 - Full Wave, Capacitor Input Filter Rectifier
The transformer is rated at 60VA and has a primary resistance of 4.3 Ohms, and a secondary resistance of 0.5 Ohms. This calculates to an internal copper loss resistance of 1.0 Ohm.
With a 20 Ohm load as shown and at an output current of 1.57A, diode conduction is about 3.5ms, and the peak value of the current flowing into the capacitor is 4.8A - 100 times per second (10ms interval). Diode conduction is therefore 35% of the cycle. RMS current in the transformer secondary is 2.84A.
Secondary AC Amps 2.84A RMS 6.4A Peak Secondary AC Volts (loaded) 25.9V RMS 34.1V Peak Secondary AC Volts (unloaded) 28.0V RMS 39.6V Peak DC Current 1.57A Capacitor Ripple Current 2.36A DC Voltage (loaded) 31.6V DC Voltage (unloaded) 38.3V DC Ripple Voltage 692mV RMS 2.2V Peak-Peak
Ripple across the load is 2.2V peak-peak (692mV RMS), and is the expected sawtooth waveform. Average DC loaded voltage is 31.6V. The no-load voltage of this supply is 38.3V, so at a load current of 1.57A, the regulation is ...
Reg (%) = (( Vn - Vl ) / Vn ) × 100
Where Vn is the no-load voltage, and Vl is the loaded voltage
For this example, this works out to close enough to 17% which is hardly a good result. By comparison, the actual transformer regulation would be in the order of 8% for a load current of 2.14A at 28V. Note that the RMS current in the secondary of the transformer is 2.84A AC (approximately the DC current multiplied by 1.8) for a load current of 1.57A DC - this must be so, since otherwise we would be getting something for nothing - a practice frowned upon by physics and the taxman.
Output power is 31.6V × 1.57A = 49.6W, and the input is 28V × 2.84A = 79 VA.
The input power to the transformer is 60W, so power factor is ...
PF (Power Factor) = Actual Power / Apparent Power = 60 / 79 = 0.76
There are many losses to account for, with most being caused by the diode voltage drop (600mW each diode - 2.4W total) and winding resistance of the transformer (8W at full load). Even the capacitors ESR (equivalent series resistance) adds a small loss, as does external wiring. There is an additional loss as well - the transformer core's 'iron loss' - being a combination of the current needed to maintain the transformer's flux level, plus eddy current losses which heat the core itself. Iron loss is most significant at no load and can generally be ignored at full load.
Even though the transformer is overloaded for this example, provided the overload is short-term no damage will be caused. Transformers are typically rated for average power (VA), and can sustain large overloads as long as the average long-term rating is not exceeded. The duration of an acceptable overload is largely determined by the thermal mass of the transformer itself.
 |
Capacitor Ripple Current - It is well known that bigger transformers have better efficiency that small ones, so it is a common practice to use a
transformer that is over-rated for the application. This can improve the regulation considerably, but also places greater stresses on the filter capacitor due to higher
ripple current. This is quoted in manufacturer data for capacitors intended for use in power supplies, and must not be exceeded. Excessive ripple current will cause
overheating and eventual failure of the capacitor.
Large capacitors usually have a higher ripple current rating than small ones (both physical size and capacitance). It is useful to know that two 4,700µF caps will usually have a higher combined ripple current than a single 10,000µF cap, and will also show a lower ESR (equivalent series resistance). The combination will generally be cheaper as well - one of the very few instances where you really can get something for nothing. |
For further reading on this topic, see the Linear Power Supply Design article.
If I never hear someone complaining that "distortion measurements are invalid, and a waste of time" again, it will be too soon. I am so fed up with self-proclaimed experts (where 'x' is an unknown quantity, and a 'spurt' is a drip under pressure) claiming that 'real world' signals are so much more complicated than a sinewave, and that static distortion measurements are completely meaningless. Likewise, some complain that sinewaves are 'too simple', and that somehow they fail to stress an amplifier as much as music will.
Measurements are not meaningless, and real world signals are sinewaves! The only difference is that with music, there is usually a large number of sinewaves, all added together. There is not a myriad of simultaneous signals passing through an amp, just one (for a single channel, naturally).
Since physics tells us that no two masses can occupy the same physical space at the same time, so it is with voltages and currents. There can only ever be one value of voltage and one value of current flowing through a single circuit element at any instant of time - if it were any different, the concept of digital recording could never exist, since in a digital recording the instantaneous voltage is sampled and digitised at the sampling rate. This would clearly be impossible if there were say 3 different voltages all present simultaneously.
So, how do these x-spurts determine if an amplifier has a tiny bit of crossover distortion (for example). I can see it as the residual from my distortion meter, and it is instantly recognisable for what it really is, and I can see the difference when I make a change to a circuit to correct the problem. If I had to rely on my ears (which although getting older, still work quite well), It would take me much longer to identify the problem, and even longer to be certain that it was gone. I'm not talking about the really gross crossover distortion that one gets from an under-biased amp, I am referring to vestiges - miniscule amounts that will barely register on the meter - I use my oscilloscope to see the exact distortion waveform. I suspect that this dilemma is 'solved' by some by simply not using the push-pull arrangement at all, thereby ensuring that power is severely limited, and other distortion is so high that they would not dare to publish the results.
These same x-spurts may wax lyrical about some really grotty single ended triode amp, with almost no power and a highly questionable output transformer, limited frequency response and a damping factor of unity if it is lucky.
Don't get me wrong - I'm not saying that this is a definition of single-ended triode amps (for example), there are some which I am sure sound very nice - not my cup of tea, but 'nice'. I have seen circuits published on the web that I would not use to drive a clock radio speaker (no names, so don't ask), and 'testimonials' from people who have purchased this rubbish, but there are undoubtedly some that do use quality components and probably sound ok at low volume levels.
Sorry if I sound vehement (vitriolic, even), but quite frankly this p****s me off badly. There are so many people waving their 'knowledge' about, and many of them are either pandering to the Magic Market, or talking through their hats.
The whole idea of taking measurements is to ensure that the product meets some quality standard. Once this standard is removed and we are expected to let our ears be the judge, how are we supposed to know if we got what we paid for? If the product turns out to sound 'bad', should we accept this, or perhaps we should listen to it for long enough that we get used to the sound (this will happen - eventually - it's called 'burn-in' by the subjectivists). I am not willing to accept this, and I know that many others feel the same.
Please don't think that I am advocating specsmanship, because I'm not. I just happen to think that consumers are entitled to some minimum performance standard that the equipment should meet (or exceed). I have yet to hear any amplifier with high distortion levels and/or limited bandwidth sound better than a similar amplifier with lower distortion and wider bandwidth. This implies that we compare like with like - a comparison between a nice valve amp and a nasty transistor amp will still show the transistor amp as having better specs, but we can be assured that it will sound worse. In similar vein, a nice transistor amp compared against a rather poor valve amp may cause some confusion, often due to low damping from the valve amp which makes it easy to imagine that it sounds 'better'.
We need measurements, because they tell us about the things that we often either can't hear, or that may be audible in a way that confuses our senses. Listening tests are also necessary, but they must be properly conducted as a true blind A-B test or the results are meaningless. Sighted tests (where you know exactly which piece of gear you are listening to) are fatally flawed and will almost always provide the expected outcome.
This is an argument that has been going for years, and it seems we are no closer to resolving the dilemma than we ever were. I have worked with all three, and each has its own sonic quality. Briefly, we shall have a look at the differences - this is not an exhaustive list, nor is it meant to be - these are the main points, influenced by my own experiences (and I must admit, prejudices). Please excuse the somewhat random order of the comparisons ...
Valves:
Valves are Voltage to Current Converters, so the output current is controlled by an input voltage. It is necessary to apply the varying output current to a load (the anode resistor or transformer) to derive an output voltage.
- Valves themselves are inherently passably linear, and can operate with no feedback at all within a restricted range, and still provide a high quality signal. The range is usually more than sufficient for preamps, but is pushed to its limits in power amplifiers.
- Relatively low gain per device, meaning that more are needed, or less feedback can be used.
- 'Soft' distortion characteristics, meaning that most of the distortion is low order (including crossover distortion and clipping) - this is not (quite) as obtrusive or fatiguing as 'hard' distortion.
- Distortion onset is gradual, and effectively warns the listener that the limits are being approached by losing clarity, but in a manner that is not too obtrusive.
- Distortion is usually measurable at nearly any power level, but is low order (mainly 2nd and 3rd harmonics - small amounts of additional harmonics are usually also present).
- Limited feedback, mainly due to the fact that the output transformer introduces low and high frequency phase shift, so large amounts of global feedback are generally not possible without oscillation. This results in a (comparatively) limited bandwidth.
- High output impedance, meaning that damping factor in power amps is generally rather poor. Extremely low values of output impedance are very difficult to achieve (although it can be done at considerable extra expense).
- Valves have a perfect dielectric (mainly a vacuum, with some mica), leading to a highly linear Miller capacitance - it is unknown if this contributes any audible benefit.
- Inefficient output stage, allowing the amp to sound louder than it really is on a watt for watt basis. This may sound like a contradiction, but a valve amp has a 'compliant' output, that allows it to provide a larger voltage swing to high impedance loads (such as a loudspeaker driver at resonance).
- Fairly rugged, and can withstand short circuits without damage - BUT open circuits can cause the output transformer to create high flyback voltages that can cause insulation breakdown in the transformer windings or the valve sockets (short circuits are OK, open circuits are bad)
- Usually quite tolerant of difficult loads, such as electrostatic loudspeakers.
- A wonderful nostalgia value, which allows people to accept the shortcomings, and truly believe that the amp really does sound better than a really good solid-state unit. Proper double-blind testing will usually reveal the truth - provided that the solid-state equivalent is modified to match the output impedance of the valve unit!
Transistors (BJTs):
By default, bipolar transistors are Current to Current Converters. This means that they use an input current change to derive an output current change that is greater than the input (therefore amplification occurs). Again, it is necessary to use a resistor or other load to allow an output voltage to be developed. It's worth noting that in some texts you will see that the author insists that transistors are voltage controlled, but I find this to be at odds with reality. I have always worked with them as current controlled devices, and will continue to do so.
- Transistors are also quite linear within a restricted range, but due to the lower operating voltages usually cannot successfully be used without feedback if a very high quality signal is desired, even in preamp stages.
- High to very high gain per device, allowing local feedback to linearise the circuit before the application of global feedback.
- Onset of distortion is sudden and without warning in most feedback topologies.
- Low to very low distortion, provided clipping is not introduced. This creates both the low order harmonics of the valve amp, plus high order harmonics which may be very fatiguing.
- Wide to very wide bandwidth, and low phase shift, largely due to the elimination of the output transformer. The wide bandwidth is obviously an advantage, the phase response is highly debatable as to its overall value to the listener.
- Usually large amounts of global feedback, which is needed to linearise the output stage, especially at the crossover point between output devices (0 Volts) for power amplifiers.
- Completely oblivious to open circuit loads, but must be protected against instant damage with short circuited outputs (open circuits are OK, short circuits are bad - i.e. the opposite of valves)
- The Miller capacitance of transistors has an imperfect dielectric, and varies with applied voltage. This might be the reason that some transistor amps can be seen to oscillate at a specific voltage level (small bursts of oscillation on the waveform, but only above a certain voltage across the device). Tricky.
- Intolerant of difficult loads, unless extensive measures are taken to ensure stability. This can increase complexity quite dramatically.
MOSFETs:
Like valves, MOSFETs are voltage to current converters, and rely on a voltage on the gate to control the output current. As before, a resistor or other load converts the varying current into a voltage. Here I discuss lateral (designed for audio) MOSFETs, not switching types. HEXFETs and similar switching MOSFETs (vertical MOSFETs) are not really suited to linear operation, and have some interesting failure mechanisms just waiting to bite you. So, for lateral MOSFETs ...
- Similar to most of the comments about bipolar transistors, with the following differences:
- Onset of (clipping) distortion is (usually) not quite as savage as transistors, but is much more sudden than valves. This is a very minor difference, and can safely be ignored.
- May not be as linear as valves or bipolar transistors, especially near the cutoff region. Big differences between different types (lateral/ vertical)
- More efficient than valves, but not as efficient as bipolar transistors. There will always be less output voltage swing available from a MOSFET amp than a bipolar transistor amp (for the same supply voltage), unless an auxiliary power supply is used.
- Gain is (usually) higher than valves, but lower than bipolar transistors - limiting the ability to apply local feedback, and even overall (global) feedback may not produce distortion figures as good as bipolar transistors - especially with vertical MOSFETs.
- Low distortion (lateral types), but may require more gain in the preceding stages to allow sufficient feedback to eliminate crossover distortion.
- Very wide bandwidth (better than bipolar transistors), allowing less compensation and full power operation up to 100 kHz in some amps - the value of this is debatable.
- More rugged than bipolar transistors, and do not suffer from second breakdown effects - fuses can be used for short circuit protection, and no open circuit protection is needed.
- Reasonably tolerant of difficult loads without excessive circuit complexity.
To complicate matters, there are two main types of MOSFET as stated at above - lateral and vertical. This applies to the internal construction. Lateral MOSFETs are well suited to audio (see Project 101), while vertical (e.g. HEXFETs) are designed for high speed switching, and are not really suitable for audio. Despite this, it is possible to make an amplifier using HEXFETs that performs well, and this has been achieved by many hobbyists and manufacturers.
Thermal stability is critical with vertical MOSFETs, and a very good bias servo is essential. Because of their high transconductance (and wide parameter spread), when used in parallel for audio they need to be matched for gate threshold voltage. If this isn't done, the device with the lowest gate threshold will take most of the current, causing it to get hotter, meaning that it will take even more of the current. This will lead to output stage failure.
Lateral MOSFETs do not have this problem, because they have a relatively high RDS-On (on resistance), and they share current well despite gate threshold voltage differences.
Because of the differences outlined above it is very important to compare like with like, since each has its own strengths and problems. Also, each of the solid state amp types has its niche area, where it will tend to outperform the other, regardless of specifications. The valve amp is the odd man out here, as it is far more likely to have devoted fans who would use nothing else - most solid state amp users are (or should be) a pragmatic lot, using the most appropriate configuration for the intended application.
There is no such thing at the time of writing as the much sought after (but elusive) 'straight wire with gain'. But wait - there's more ....
Another aspect of amplifier design is slew rate. Slew-rate simply refers to the rate of change of voltage in a given time. It's typically quoted in volts per microsecond (V/µs). This term and (more to the point) its effects are not well understood, and the possible effects are often taken to extremes to 'prove' a point. In reality, no competent amplifier will show any sign of 'slew induced distortion' or undesirable behaviour with any normal music signal. Virtually any amplifier can be forced into slew-rate limiting if pushed to a high enough frequency at full power.
It has been claimed by many writers on the subject that a slew-rate limited amplifier will introduce transient intermodulation distortion, or TIM (aka TID - transient induced distortion). In theory, this is perfectly true, provided that the slew rate is sufficiently low as to be within the audible spectrum (i.e. below 20 kHz), and the program material has sufficient output voltage at high frequencies to cause the amplifier to limit in this fashion.
The following nomograph is helpful in allowing you to determine the required slew rate of any amplifier, so that it can reproduce the required audio bandwidth without introducing distortion components as a result of not being fast enough.
Figure 14 - Slew Rate Nomograph
To use this nomograph, first select the maximum frequency on the top row. Let's assume 30kHz as an example. Next, select the actual output voltage (peak, which is RMS × 1.414) that the amplifier must be able to reproduce. For a 100W 8 Ohms amp, this is 28V RMS, or 40V peak. Now draw a line through these two points as shown, and read the slew rate off the bottom row. For the example, this is 8V/µs. This is in fact far in excess of what is really needed, since it is not possible for an amp reproducing music to have anywhere near full power at 30kHz.
By 20kHz, our 100W amp will need an output of perhaps 10W (typically much less), and this is only about 12V peak. Using the nomograph with this data reveals that a slew rate of about 2V/µs is quite sufficient. Such an amp will go into what is known as slew-rate limiting at full power with frequencies above 10kHz or so, converting the input sinewave into a triangular wave whose amplitude decreases with increasing frequency.
Some claim that this is audible, and although this is largely subjective it can be measured by a variety of means. That a typical audio signal is a complex mixture of signals is of no real consequence, because an amp has no inherent concept of 'complex' any more than it has an opinion about today's date or the colour of your knickers. At any given point in time, there is an instantaneous value of input voltage that must be increased in amplitude and provide the current needed to drive the loudspeaker. As long as this input voltage does not change so fast that the amplifier cannot keep up with the change then little or no degradation should occur, other than (hopefully) minor non-linearities that represent distortion.
Although this is a fine theory, there seems to be much entrenched prejudice against 'slow' amplifiers. Whether they sound different from another that is not constrained by slew rate limiting within the full audible range remains debatable. These differences are easily measured, but may be irrelevant when the system is used for music, which simply does not have very fast rise or fall times.
As shown above, the slew rate of an amplifier is usually measured in Volts / microsecond, and is a measure of how fast the amplifier's output can respond to a rapidly changing input signal. Few manufacturers specify slew rate these days (mainly because few buyers understand what it is), but it is an important aspect of an amplifier's design. It's also important to understand that music never contains any signals that produce full power at 10 or 20kHz. It's generally accepted that the amplitude falls at ~6dB/octave above 1-2kHz, so a 100W amp with a peak output of 40V won't be called upon to provide much above 5V (peak) at 20kHz. There will always be exceptions, and it's safer to assume and plan for at least 10V peak at 20kHz. More doesn't hurt anything, but usually doesn't make an audible difference (assuming a proper double blind test of course).
As can be seen from the above, for an amplifier (of any configuration) to reproduce 28V RMS at 20 kHz (about 100W / 8 Ohms) requires a slew rate of 4.4 V / µs. This is to say that the output voltage can change (in either direction) at the rate of 8 Volts in one microsecond. This is not especially fast, and as should be obvious, is dependent upon output voltage. A low power amp need not slew as fast as a higher powered amp. There is no real requirement for any amp to be able to slew faster than this, as there is a significantly large margin provided already. This can be calculated or measured.
Doubling the amplifier's output voltage (four times the power) requires that the slew rate doubles, and vice versa, so a 400W amp needs a slew rate of 8.8 V / µs, while a 25W amp only needs 2.2 V /µs. This is a very good reason to use a smaller amplifier for tweeters in a triamped system, since it is much easier to achieve a respectable slew rate when vast numbers of output devices are not required.
Essentially, if the amplifier's output cannot respond to the rapidly changing input signal, an error voltage is developed at the long-tailed pair stage, which tries to correct the error. The LTP is an amplifier, but more importantly, an error amplifier, whose sole purpose is to keep both of its inputs at the same voltage. This is critical to the operation of a solid state amp, and the LTP output will generally be a very distorted voltage and current waveform, producing a signal that is the exact opposite of all the accumulated distortions within the remainder of the amp (this also applies to opamps).
The result is (or is supposed to be) that the signal applied to the inverting input is an inverted exact replica of the input signal. Were this to be achieved in practice, the amp would have no distortion at all. In reality, there is always some small difference, and if the Class-A driver or some other stage enters (or approaches) the slew rate limited region of operation, the error amp (LTP) can no longer compensate for the error.
Once this happens distortion rises, but more importantly, the input signal is exceeding the capabilities of the amplifier, and the intermodulation products rise dramatically. Intermodulation distortion is characterised by the fact that a low frequency signal modulates the amplitude (and / or shape) of a higher frequency signal, generating additional frequencies that were not present in the original signal. This also occurs when an amplifier clips, or if it has measurable crossover distortion.
Sounds like ordinary distortion, doesn't it? That too creates frequencies that were not in the original, but the difference is that harmonic distortion creates harmonics (hence the name), whereas intermodulation distortion creates frequencies that have no harmonic relationship to either of the original frequencies. Rather, the new frequencies are the sum and difference of the original two frequencies. (This effect is used extensively in radio, to create the intermediate frequency from which the audio, video or other wanted signal can be extracted.) The term 'harmonic' basically can be translated to 'musical', and 'non-harmonic' is mathematically derived, but not musically related .... if you see what I mean.
Whenever the LTP (error amplifier) loses control of the signal, intermodulation products will be generated, so the bandwidth of an amplifier must be wide enough to ensure that this cannot happen with any normal audio input signal. There is nothing wrong or difficult about this approach, and it is quite realisable in any modern design. Although unrealistic from a musical point of view, it is better if an amplifier is capable of reproducing full power at the maximum audible frequency (20 kHz) than if it starts to go into slew rate limiting at some lower frequency.
The reason I say it is unrealistic musically is simply because there is no known instrument - other than a badly set up synthesiser - that is capable of producing any full power harmonic at 20 kHz, so in theory, the amp does not have to be able to reproduce this. In reality, inability to reproduce full power at 20 kHz means that the amp might suffer from some degree of transient intermodulation distortion with some program material. Or it might not.
This is not a problem that affects simple amps with little or no feedback - they generate enough harmonic distortion to more than make up for the failings of more complex circuits with lots of global feedback. This fact tends to annoy the minimalists, who are often great believers in no feedback under any circumstance, which relegates them to listening to equipment that would have been considered inferior in the 1950s.
If preferred, you can calculate the slew rate of any signal at any amplitude. Use the formula ...
ΔV / Δt = 2π × f × VPeak
ΔV / Δt is the slew rate (change of voltage vs change of time). VPeak is the peak voltage of the sinewave. For example, if you use a voltage of 40V (peak) and a frequency of 20kHz, you get 5,026,548V/s, which is (close enough to) 5.03V/µs.
Few sensible people would argue that measurements of frequency response are unimportant or irrelevant, and this is one of the simplest measurements to take on an amplifier. Again, the subjectivists would have it that these fail to take into account some mysterious area of our brain that will compensate for a restricted response, and allow us to just enjoy the experience of the sound system. This is true - we will compensate for diminished (or deranged) frequency response, but it need not be so.
If you listen to a clock radio for long enough, your brain will think that this is normal, and will adjust itself accordingly. Imagine your surprise when you hear something that actually has real low and high frequencies to offer - the first reaction is that there is too much of everything, but again, the brain will make the required allowances and this will sound normal after a time.
There are so many standard measurements on amplifiers that are essential to allow us to make an informed judgement (is this amp even worth listening to?). I really object to the attitude that "it does not matter what the measurements say, it sounds great". In reality this is rarely the case - if it measures as disgusting, then it will almost invariably sound disgusting. There is no place for hi-fi equipment that simply does not meet some basic standards - and I have never heard an amp that looked awful on the oscilloscope, measured as awful on my distortion meter, but sounded good - period. I have heard some amps that fall into that category that sound 'interesting' - not necessarily bad, but definitely not hi-fi by any stretch of the imagination. To the dyed-in-the-wool subjectivist, it seems that 'different' means 'better', regardless of any evidence one way or another.
There are some designs that should simply be avoided. Two in particular are shown here, but this doesn't mean that there aren't others as well. The two shown below suffer from a number of problems, with the biggest issue being thermal stability. This is by no means all though - the first to avoid is shown in Figure 14, and includes a compound (Sziklai) pair for comparison. As you can see, the 'output stage with gain' (output 1) simply breaks the feedback loop within the compound pair and adds resistors. The gain is directly proportional to the resistor divider ratio, so the gain is 3.2 with 220 ohms and 100 ohms as shown. The problem is that this applies to DC as well as AC, so the stage amplifies its own thermal instability. Because of the relatively high output impedance, the actual gain will be less than calculated.
Figure 15 - Output Stage with Gain (Sziklai Pair for Comparison)
Why would anyone bother? The stage has the advantage that having gain, so it can be driven directly by an opamp whose output level would normally be too low to be useful. Several amplifiers have been built using this circuit over the years, and all those I have seen have been thermally unstable, and some also have high frequency instability issues. Because the output stage local feedback is reduced by the amount of gain used, distortion is significantly higher than with a conventional compound pair (for example). In the above circuits, the stage with gain has an open loop distortion of 4%, while the compound pair stage has distortion less than 0.1%. This was simulated using an 8 ohm load - in reality, the distortion difference is usually greater than this, with the gain version showing even higher distortion. A vast amount of negative feedback is needed to make the circuit linear enough to be usable. As noted above, output impedance is also much higher than the compound pair.
If the circuit is driven by an opamp, the opamp's high gain helps to linearise the output stage, but high frequency instability remains an issue. It can be solved, but usually requires several HF stability networks. Such arrangements are usually easy to coax into oscillation because they tend to have a poor phase margin (the difference between the actual phase shift and 180°, where the amp will oscillate).
There is no simple cure for the thermal instability though. A single transistor cannot compensate for the quiescent current shift, and a Darlington pair overcompensates. While it is certainly possible to come up with a composite circuit that will work, the complexity is not warranted for an output stage that doesn't perform well at the best of times.
Another travesty was unleashed many years ago, and fortunately I've not seen it re-surface for many years. I am almost unwilling to post the circuit, lest someone think it's a good idea. It isn't a good idea, and never was. Again, thermal instability was a major problem, and HF instability was also common. The idea was to use an opamp's supply pins to drive output transistors. By loading the opamp, the supply current varies from a couple of milliamps at idle, up to perhaps 20-30mA (depending on the opamp). An example circuit of this disaster is shown below.
Figure 16 - Opamp Based Power Amplifier
If you happen to see this circuit (or any of its variations) anywhere, avert your eyes immediately  . I recall messing around with it some time in the 1970s, and while it was (barely) possible to make it reasonably stable (against HF instability), the only way to achieve thermal stability is to use relatively large resistors in the output transistor emitters. This limits the output power, but it is capable of driving headphones, provided you can live with it's other failings which are many and varied. Since there are so many circuits that outperform it (including cheap and cheerful 'power opamps' - IC power amps), there is no reason to consider it for anything other than your own amusement.
. I recall messing around with it some time in the 1970s, and while it was (barely) possible to make it reasonably stable (against HF instability), the only way to achieve thermal stability is to use relatively large resistors in the output transistor emitters. This limits the output power, but it is capable of driving headphones, provided you can live with it's other failings which are many and varied. Since there are so many circuits that outperform it (including cheap and cheerful 'power opamps' - IC power amps), there is no reason to consider it for anything other than your own amusement.
Note that the values shown on these circuits are for example only. I cannot guarantee that the opamp based amp will even work as shown - the circuit is there only so you can see the general arrangement. Since I strongly suggest that you stay well clear of this topology, I do not propose to waste time to ensure that the circuit will function as shown.
For further reading, I can recommend The Self Site, and in particular 'Science and Subjectivism in Audio' and also my own article on the subject Cables, Interconnects & Other Stuff - The Truth. There is also an article called Amplifier Sound - What Are The Influences? that goes a little deeper into the measured and subjective performance of amplifiers, and suggests a couple of new tests that might be applied.
 Main Index
Main Index
 Articles Index
Articles Index